如图,点A、D在射线AE上,直线AB∥CD,∠CDE=140°,那么∠A的度数为( )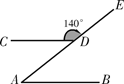
A.140° B.60° C.50° D.40°
已知三角形的两边长分别为 和
和 ,则此三角形的第三边长可以是( )
,则此三角形的第三边长可以是( )
A. |
B. |
C. |
D. |
一个多边形的每一个内角均为108°,那么这个多边形是( )
| A.七边形 | B.六边形 | C.五边形 | D.四边形 |
下列运算正确的是( )
A.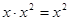 |
B.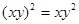 |
C. |
D. |
下列各式能用平方差公式计算的是( )
A. |
B. |
C. |
D. |
2015年2月1日宿迁市最高气温是8℃,最低气温是-2℃,则当天宿迁市气温变化范围t(℃)是( )
| A.t>8 | B.t<2 | C.-2<t<8 | D.-2≤t≤8 |
下列语句中,属于定义的是( )
| A.两点确定一条直线 |
| B.两直线平行,同位角相等 |
| C.两点之间线段最短 |
| D.直线外一点到直线的垂线段的长度,叫做点到直线的距离 |
如图,两个正方形的边长分别为 和
和 ,如果
,如果 ,
, ,那么阴影部分的
,那么阴影部分的
面积是( )
A. |
B. |
C. |
D. |
如果不等式组 无解,那么m的取值范围是 ( )
无解,那么m的取值范围是 ( )
| A.m>8 | B.m≥8 | C.m<8 | D.m≤8 |
利用两块长方体木块测量一张桌子的高度.首先按图①方式放置,再交换两木块的位置,按图②方式放置.测量的数据如图,则桌子的高度是 ( ) 
| A.73cm | B.74cm | C.75cm | D.76cm |
分解因式:a 3-9a﹦ .
用科学记数法表示0.000031的结果是 .
把方程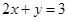 改写成用含
改写成用含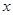 的式子表示y的形式,得
的式子表示y的形式,得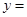 .
.
已知 是方程2x+ay=6的解,则
是方程2x+ay=6的解,则 .
.
如图,将边长为 的等边△
的等边△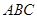 沿边
沿边 向右平移
向右平移 得到△
得到△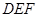 ,则四边形
,则四边形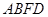 的周长为
的周长为 
“对顶角相等”的逆命题是_________命题(填真或假)。
计算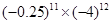
 .
.
如图,△ 中,点
中,点 是
是 上的一点,
上的一点, ,
, 是
是 中点, 点F是BD的中点。若△
中点, 点F是BD的中点。若△ 的面积
的面积 ,则
,则 .
.
如图,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC外,若∠2=20°则∠1的度数为 度.
如图,数轴上,点A的初始位置表示的数为1,现A做如下移动:第1次点A向左移动3个单位长度至点 ,第2次从点
,第2次从点 向右移动6个单位长度至点
向右移动6个单位长度至点 ,第3次从点
,第3次从点 向左移动9个单位长度至点
向左移动9个单位长度至点 ,…,按照这种移动方式进行下去,对于点
,…,按照这种移动方式进行下去,对于点 ,当n=2015时,这个点表示的数是 .
,当n=2015时,这个点表示的数是 .
(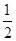 )-3-22×0.25-
)-3-22×0.25-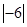 +(
+(
(6分)解方程组 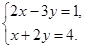
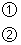
解不等式 ,并求它的非负整数解.
,并求它的非负整数解.
解不等式组: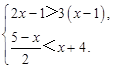
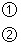
请将下列证明过程补充完整:
已知:如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,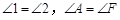 .
.
求证: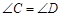 .
.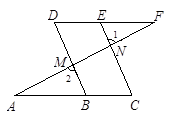
证明:因为 (已知),
(已知),
又因为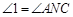 ( ),
( ),
所以 (等量代换).
所以 ∥ (同位角相等,两直线平行),
所以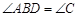 ( ).
( ).
又因为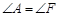 (已知),
(已知),
所以 ∥ ( ).
所以 (两直线平行,内错角相等).
所以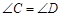 ( ).
( ).
学生问老师:“您今年多大?”老师风趣地说:“我像你这么大时,你才2岁;你到我这么大时,我已经38岁了.”老师今年多大了?
关于x的不等式组 有21个整数解,则a的取值范围是 .
有21个整数解,则a的取值范围是 .
(10分)如图,四边形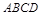 中,
中,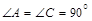 ,
,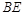 平分
平分 交
交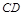 于
于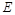 ,
,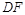 平分
平分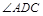 交
交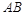 于
于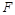 .
.
(1)若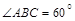 ,则
,则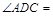 °,
°,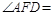 °;
°;
(2)求证:BE∥DF
(1)有甲、乙、丙三种商品,如果购甲3件、乙2件、丙1件共需15元,如果购甲1件、乙2件、丙3件共需25元,那么购甲、乙、丙各1件共需多少元?
(2)已知2a+b+3c=15,3a+b+5c=25,则a+b+c=
(3)已知2a+b+xc=15,3a+b+yc=25, 要想求出a+b+c的值,x与y必须满足的关系是?