在平面直角坐标系中，点P（2，－3）所在的象限是（ ）．
A．第一象限 B．第二象限 C第三象限 D．第四象限
下列各数中，无理数是（ ）．
A． |
B． |
C． |
D． |
的平方根是（ ）．
| A．±4 | B．4 | C．±2 | D．2 |
二元一次方程x-2y=1有无数多组解，下列四组值中不是该方程解的是（ ）．
A． |
B． |
C． |
D． |
若
，则下列式子中错误的是（ ）．
A． |
B． |
C． |
D． |
不等式组
的解集在数轴上表示正确的是（ ）．
下列说法正确的是（ ）．
| A．“邻补角相等吗？”是一个命题 |
| B．“同位角相等”是假命题 |
| C．“相等的角是对顶角”是真命题 |
| D．“如果两条直线不相交，那么一定平行”是真命题 |
如图，能判定AB∥CD的条件是（ ）．
| A．∠ACB+∠B＝180° |
| B．∠ACD＝∠B |
| C．∠ACD＝∠A |
| D．∠DCE＝∠A |
如图，已知点O在直线AB上，OC为射线，∠1比∠2的3倍少10°．设∠1，∠2的度数分别为x，y，那么能正确求出这两个角度数的方程是（ ）．
A． |
B． |
C． |
D． |
端午节期间，某餐厅推出了四种粽子新款（分别以A、B、C、D表示），请顾客免费试吃后选出最喜欢的品种．结果反馈如下：
C D D A A B A B B B A
C C A A B A A C D C D
下列说法正确的是（ ）．
A．A款粽子最受欢迎
B．B款粽子比C款粽子更受欢迎
C．喜欢C，D两款粽子的人加起来占样本的一半
D．D款粽子受欢迎程度仅次于C款
、
、−4、0这四个数中，最大的数是 ；
若x－y＝2，则7－x＋y＝ ；
不等式
的非负整数解是 ；
如图，
是由
沿射线
方向平移2cm得到，若＝3cm，则
＝ cm．
如图，已知点M，N，G为同一平面直角坐标系中的三点，若点M的坐标为（2，-2），
点N的坐标为（4，-1），则G的坐标为 ；
一个容量为80的样本最大值是143，最小值是50，在绘制频数直方图时取组距为10，则可以分成 组．
计算：
．
解不等式
，并把解集在数轴上表示出来．
如图，EF∥BC，AC平分∠BAF，∠B=80°．求∠C的度数．
已知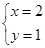
是二元一次方程组
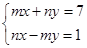的解，求m+3n的立方根．
△ABC在平面直角坐标系中的位置如图所示，其中每个小正方形的边长为1个单位长度．将△ABC向左平移3个单位长度，再向下平移2个单位长度得到△A1B1C1．
（1）写出△ABC的顶点坐标；
（2）请在图中画出△A1B1C1．
为了解某校学生的身高情况，随机抽取该校男生、女生进行抽样调查．已知抽取的样本中，男生、女生的人数相同，利用所得数据绘制如下统计图表：
根据图表提供的信息，回答下列问题：
（1）本次调查的学生人数为___________人；
（2）样本中，女生身高E组所占的圆心角的度数为 度；
（3）已知该校共有男生400人，女生380人，请估计身高在160≤
<170之间的学生约有多少人？
某文具商场销售A、B两种品牌书包，两种书包的进货价格分别为每个30元，40元．商场销售5个A品牌和1个B品牌书包，可获利76元；销售6个A品牌和3个B品牌书包，可获利120元．
（1）求商场销售A、B两种品牌书包的销售价格分别是多少元？（利润＝销售价格－进货价格）
（2）商场准备用不多于2500元的资金购进A、B品牌书包共70个，问最少需要购进A种品牌的书包多少个？
如图，已知AB∥DE，∠B=60°，AE⊥BC，垂足为点E．
（1）求∠AED的度数；
（2）当∠EDC满足什么条件时，AE∥DC，证明你的结论．
如图，在下面直角坐标系中，已知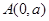
、
、
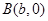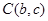三点，其中a、b、c满足关系式
，
．
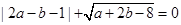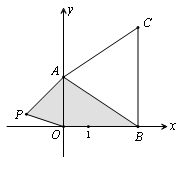
（1）请写出a、b、c的值．
（2）若点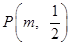
在第二象限，请用含m的式子表示四边形
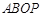的面积；
（3）在（2）的条件下，是否存在点P，使四边形
的面积与△
的面积相等？若存在，请求出点P的坐标，若不存在，请说明理由．