已知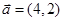 ,
, ,若
,若 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
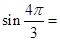 ( )
( )
A. |
B. |
C.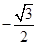 |
D.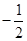 |
采用系统抽样的方法从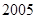 个个体中抽取一个容量为
个个体中抽取一个容量为 的样本,则抽样间隔和随机剔除的个体数分别为( )
的样本,则抽样间隔和随机剔除的个体数分别为( )
A.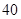 , , |
B. , , |
C. , ,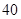 |
D. , , |
函数 在区间
在区间 的简图是( )
的简图是( )
甲、乙两战士进行射击比赛,甲不输的概率为 ,乙输的概率为
,乙输的概率为 ,则甲不赢的概率和甲、乙两人战平概率分别是( )
,则甲不赢的概率和甲、乙两人战平概率分别是( )
A.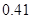 , ,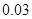 |
B. , ,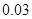 |
C.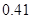 , , |
D. , , |
某校高一( )班共有
)班共有 人,如图是该班期中考试数学成绩的频率分布直方图,则成绩在
人,如图是该班期中考试数学成绩的频率分布直方图,则成绩在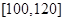 内的学生人数为( )
内的学生人数为( )
A. |
B. |
C. |
D. |
某中学高一有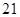 个班、高二有
个班、高二有 个班、高三有
个班、高三有 个班,现采用分层抽样的方法从这些班中抽取
个班,现采用分层抽样的方法从这些班中抽取 个班对学生进行视力检查,若从抽取的
个班对学生进行视力检查,若从抽取的 个班中再随机抽取
个班中再随机抽取 个班做进一步的数据分析,则抽取的
个班做进一步的数据分析,则抽取的 个班均为高一的概率是( )
个班均为高一的概率是( )
A. |
B. |
C. |
D. |
运行如图所示的程序框图,若输出的结果是 ,则输入的
,则输入的 ( )
( )
A. |
B. |
C. |
D. |
有 人从一座
人从一座 层大楼的底层进入电梯,假设每个人自第二层开始在每一层离开电梯是等可能的,则该
层大楼的底层进入电梯,假设每个人自第二层开始在每一层离开电梯是等可能的,则该 人在不同层离开电梯的概率是( )
人在不同层离开电梯的概率是( )
A. |
B. |
C. |
D. |
某商店对每天进店人数 与某种商品成交量
与某种商品成交量 (单位:件)进行了统计,得到如下对应数据:
(单位:件)进行了统计,得到如下对应数据:
 |
 |
 |
 |
 |
 |
 |
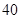 |
 |
 |
 |
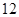 |
 |
 |
 |
 |
由表中数据,得线性回归方程为 .如果某天进店人数是
.如果某天进店人数是 人,预测这一天该商品销售的件数为( )
人,预测这一天该商品销售的件数为( )
A. B.
B. C.
C. D.
D.
为了得到函数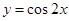 的图象,只需将函数
的图象,只需将函数 图象上所有的点( )
图象上所有的点( )
A.向右平移 个单位长度 个单位长度 |
B.向左平移 个单位长度 个单位长度 |
C.向右平移 个单位长度 个单位长度 |
D.向左平移 个单位长度 个单位长度 |
在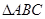 中,
中, 边上的中线
边上的中线 的长为
的长为 ,若动点
,若动点 满足
满足 (
( ),则
),则 的最小值是( )
的最小值是( )
A. |
B. |
C. |
D. |
将十进制数 化成二进制数为 .
化成二进制数为 .
在区间 上任取一个实数,则该数是不等式
上任取一个实数,则该数是不等式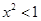 的解的概率为 .
的解的概率为 .
向量 ,
,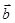 满足
满足 ,且
,且 ,
,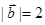 ,则
,则 在
在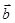 方向上的投影为 .
方向上的投影为 .
已知钝角 满足
满足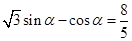 ,则
,则 .
.
化简:(Ⅰ) ;
;
(Ⅱ)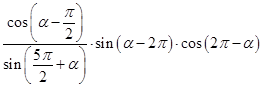 .
.
已知非零向量 ,
,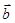 满足
满足 且
且 .
.
(Ⅰ)若 ,求向量
,求向量 ,
,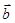 的夹角;
的夹角;
(Ⅱ)在(Ⅰ)的条件下,求 的值.
的值.
甲、乙两同学的6次考试成绩分别为:
| 甲 |
 |
 |
 |
 |
 |
 |
| 乙 |
 |
 |
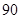 |
 |
 |
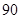 |
(Ⅰ)画出甲、乙两同学6次考试成绩的茎叶图;
(Ⅱ)计算甲、乙两同学考试成绩的方差,并对甲、乙两同学的考试成绩做出合理评价.
柜子里有 双不同的鞋,随机地取出
双不同的鞋,随机地取出 只,记事件
只,记事件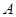 表示“取出的鞋配不成对”;事件
表示“取出的鞋配不成对”;事件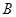 表示“取出的鞋都是同一只脚的”;事件
表示“取出的鞋都是同一只脚的”;事件 表示“取出的鞋一只是左脚的,一只是右脚的,但配不成对”.
表示“取出的鞋一只是左脚的,一只是右脚的,但配不成对”.
(Ⅰ)请列出所有的基本事件;
(Ⅱ)分别求事件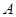 、事件
、事件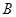 、事件
、事件 的概率.
的概率.
设向量 ,
, ,
, 为锐角.
为锐角.
(Ⅰ)若 ,求
,求 的值;
的值;
(Ⅱ)若 ,求
,求 的值.
的值.
函数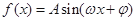 ,
, (其中
(其中 ,
,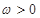 ,
, )的图象与
)的图象与 轴相邻两个交点之间的距离为,且图象上一个最低点为
轴相邻两个交点之间的距离为,且图象上一个最低点为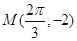 .
.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)求 的单调递增区间;
的单调递增区间;
(Ⅲ)当 时,求
时,求 的值域.
的值域.