命题“若 ,则
,则 ”的否命题是( )
”的否命题是( )
A.若 ,则 ,则 |
B.若 ,则 ,则 |
C.若 ,则 ,则 |
D.若 ,则 ,则 |
若 ,则“
,则“ ”是“
”是“ ”的( )
”的( )
| A.充要条件 | B.充分不必要条件 |
| C.必要不充分条件 | D.既不充分也不必要条件 |
在 中,角
中,角 ,
,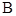 ,
,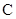 的对边长分别为
的对边长分别为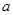 ,
,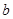 ,
,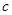 ,
, ,
,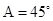 ,
,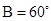 ,则
,则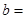 ( )
( )
A.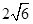 |
B. |
C.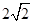 |
D. |
抛物线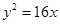 的准线方程为( )
的准线方程为( )
A.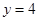 |
B. |
C.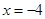 |
D.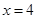 |
已知等比数列 ,
, ,
, ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
已知双曲线的渐近线方程是 ,焦点在
,焦点在 轴上,焦距为
轴上,焦距为 ,则它的方程为( )
,则它的方程为( )
A. |
B. |
C. |
D. |
已知等差数列 ,
, ,
, ,则数列
,则数列 的前
的前 项和为( )
项和为( )
A. |
B. |
C. |
D. |
设 ,
, ,若
,若 是
是 与
与 的等比中项,则
的等比中项,则 的最小值为( )
的最小值为( )
A. |
B. |
C. |
D. |
如图,空间四边形 中,
中, ,
, ,
, ,点
,点 在
在 上,且
上,且 ,点
,点 为
为 中点,则
中点,则 等于( )
等于( )

A. |
B. |
C. |
D. |
当双曲线 不是等轴双曲线时,我们把以双曲线
不是等轴双曲线时,我们把以双曲线 的实轴、虚轴的端点作为顶点的椭圆称为双曲线
的实轴、虚轴的端点作为顶点的椭圆称为双曲线 的“伴生椭圆”.则离心率为
的“伴生椭圆”.则离心率为 的双曲线的“伴生椭圆”的离心率为( )
的双曲线的“伴生椭圆”的离心率为( )
A. |
B. |
C. |
D. |
已知向量 ,
, ,
, ,若
,若 ,则
,则 .
.
不等式组 表示的平面区域的面积是 .
表示的平面区域的面积是 .
已知等差数列 ,
, ,公差
,公差 ,若
,若 ,
, ,
, 成等比数列,则
成等比数列,则 .
.
已知命题
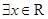 ,
, ,若命题
,若命题 是假命题,则实数
是假命题,则实数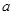 的取值范围是 .(用区间表示)
的取值范围是 .(用区间表示)
(本小题满分12分)在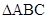 中,
中,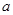 ,
,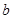 ,
,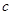 分别是角
分别是角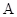 ,
,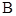 ,
,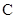 的对边,
的对边, 且
且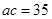 .
.
(1)求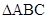 的面积;
的面积;
(2)若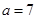 ,求角
,求角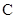 .
.
(本小题满分12分)设命题 实数
实数 满足
满足 ,其中
,其中 ,命题
,命题 实数
实数 满足
满足 .
.
(1)若 ,且
,且 为真,求实数
为真,求实数 的取值范围;
的取值范围;
(2)若 是
是 成立的必要不充分条件,求实数
成立的必要不充分条件,求实数 的取值范围.
的取值范围.
(本小题满分14分)某农场计划种植甲、乙两个品种的蔬菜,总面积不超过 亩,总成本不超过
亩,总成本不超过 万元.甲、乙两种蔬菜的成本分别是每亩
万元.甲、乙两种蔬菜的成本分别是每亩 元和每亩
元和每亩 元.假设种植这两个品种的蔬菜,能为该农场带来的收益分别为每亩
元.假设种植这两个品种的蔬菜,能为该农场带来的收益分别为每亩 万元和每亩
万元和每亩 万元.问该农场如何分配甲、乙两种蔬菜的种植面积,可使农场的总收益最大,最大收益是多少万元?
万元.问该农场如何分配甲、乙两种蔬菜的种植面积,可使农场的总收益最大,最大收益是多少万元?
(本小题满分14分)如图,在四棱柱 中,底面
中,底面 是等腰梯形,
是等腰梯形, ,
, ,
, 是线段
是线段 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)若 平面
平面 且
且 ,求平面
,求平面 和平面
和平面 所成的角(锐角)的余弦值.
所成的角(锐角)的余弦值.
(本小题满分14分)已知 为数列
为数列 的前
的前 项和,且有
项和,且有 ,
, (
( ).
).
(1)求数列 的通项公式;
的通项公式;
(2)若数列 满足
满足 ,其前
,其前 项和为
项和为 ,求证:
,求证: .
.
(本小题满分14分)已知椭圆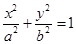 (
( )经过点
)经过点 ,且椭圆的左、右焦点分别为
,且椭圆的左、右焦点分别为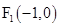 、
、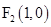 ,过椭圆的右焦点
,过椭圆的右焦点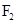 作两条互相垂直的直线,分别交椭圆于点
作两条互相垂直的直线,分别交椭圆于点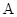 、
、 及
及 、
、 .
.
(1)求椭圆的方程;
(2)求 的值;
的值;
(3)求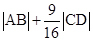 的最小值.
的最小值.