若集合 ,
, ,则
,则
A. |
B. |
C. |
D. |
如果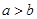 ,则下列各式正确的是
,则下列各式正确的是
A.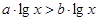 |
B. |
C. |
D.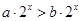 |
方程 的根
的根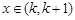 ,
,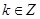 ,则
,则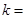
A.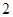 |
B.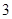 |
C.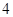 |
D.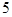 |
若角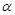 的终边过点
的终边过点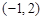 ,则
,则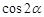 的值为
的值为
A.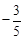 |
B.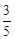 |
C.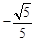 |
D.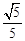 |
设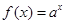 ,
,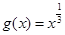 ,
,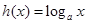 ,且
,且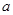 满足
满足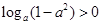 ,那么当
,那么当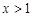 时必有
时必有
A. |
B.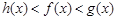 |
C.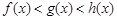 |
D. |
一个等比数列前 项的和为48,前
项的和为48,前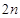 项的和为60,则前
项的和为60,则前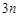 项的和为
项的和为
| A.108 | B.83 | C.75 | D.63 |
已知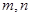 是两条不同直线,
是两条不同直线,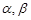 是两个不同的平面,且
是两个不同的平面,且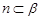 ,则下列叙述正确的是
,则下列叙述正确的是
A.若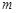 ∥ ∥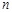 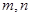 , ,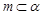 ,则 ,则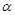 ∥ ∥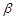 |
B.若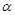 ∥ ∥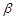 , ,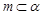 ,则 ,则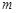 ∥ ∥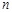 |
C.若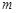 ∥ ∥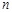 , , ,则 ,则 |
D.若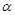 ∥ ∥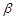 , , ,则 ,则 |
已知实数 满足约束条件
满足约束条件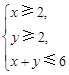 ,则
,则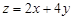 的最大值为
的最大值为
| A.24 | B.20 | C.16 | D.12 |
已知正三棱柱(底面是正三角形,且侧棱与底面垂直的棱柱)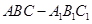 体积为
体积为 ,底面边长为
,底面边长为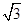 .若
.若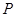 为底面
为底面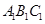 的中心,则
的中心,则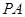 与平面
与平面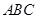 所成角的大小为
所成角的大小为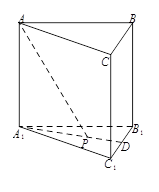
A.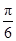 |
B.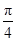 |
C.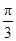 |
D.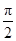 |
一个多面体的三视图如图所示,则该多面体的表面积为
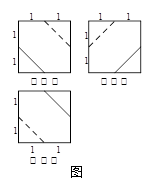
| A. |
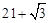
|
B. |
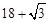
|
C. |
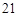
|
D. |
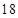
|
某工厂产生的废气经过过滤后排放,过滤过程中废气的污染物数量 与时间
与时间 间的关系为
间的关系为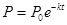 .若在前5个小时消除了
.若在前5个小时消除了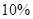 的污染物,则污染物减少
的污染物,则污染物减少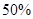 所需要的时间约为( )小时.(已知
所需要的时间约为( )小时.(已知 =0.3010,
=0.3010,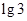 =0.4771)
=0.4771)
| A.26 | B.33 | C.36 | D.42 |
已知数列 的通项公式为
的通项公式为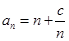 ,若对任意
,若对任意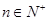 ,都有
,都有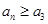 ,则实数
,则实数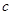 的取值范围是
的取值范围是
A.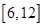 |
B.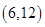 |
C.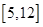 |
D.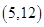 |
不等式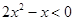 的解集为 .
的解集为 .
若等差数列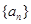 满足
满足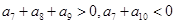 ,则当
,则当 时,数列
时,数列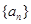 的前
的前 项和最大.
项和最大.
已知甲、乙两个圆柱的底面积分别为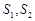 ,且
,且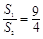 ,体积分别为
,体积分别为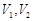 ,若它们的侧面积相等,则
,若它们的侧面积相等,则 .
.
在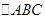 中,
中,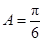 ,
,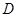 是
是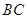 边上一点(
边上一点(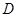 与
与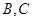 不重合),且
不重合),且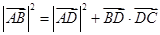 ,则
,则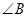 等于 .
等于 .
(本小题满分10分)已知向量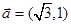 ,
,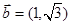 ,
,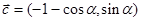 ,
,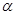 为锐角.
为锐角.
(Ⅰ)求向量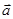 ,
,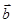 的夹角;
的夹角;
(Ⅱ)若 ,求
,求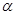 .
.
(本小题满分12分)某体育赛事组委会为确保观众顺利进场,决定在体育场外临时围建一个矩形观众候场区,总面积为 (如图所示).要求矩形场地的一面利用体育场的外墙,其余三面用铁栏杆围,并且要在体育馆外墙对面留一个长度为
(如图所示).要求矩形场地的一面利用体育场的外墙,其余三面用铁栏杆围,并且要在体育馆外墙对面留一个长度为 的入口.现已知铁栏杆的租用费用为100元
的入口.现已知铁栏杆的租用费用为100元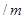 .设该矩形区域的长为
.设该矩形区域的长为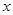 (单位:
(单位: ),租用铁栏杆的总费用为
),租用铁栏杆的总费用为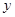 (单位:元)
(单位:元)
(Ⅰ)将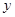 表示为
表示为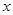 的函数;
的函数;
(Ⅱ)试确定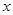 ,使得租用此区域所用铁栏杆所需费用最小,并求出最小费用.
,使得租用此区域所用铁栏杆所需费用最小,并求出最小费用.
(本小题满分12分)已知数列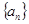 的前
的前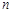 和为
和为 ,且
,且 满足:
满足: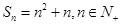 .等比数列
.等比数列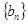 满足:
满足: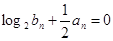 .
.
(Ⅰ)求数列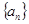 ,
,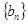 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列 的前
的前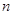 项的和
项的和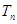 .
.
(本小题满分12分)如图,在三棱锥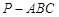 中,
中, 丄平面
丄平面 ,
,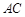 丄
丄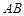 ,
, ,
, .
.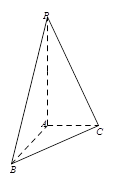
(Ⅰ)证明: 丄
丄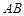 ;
;
(Ⅱ)求二面角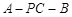 的正弦值;
的正弦值;
(Ⅲ)求三棱锥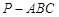 外接球的体积.
外接球的体积.
(本小题满分12分)如图,在 中,
中, ,
, ,
, 为
为 内一点,
内一点, .
.
(Ⅰ)若 ,求
,求 ;
;
(Ⅱ)若 ,求
,求 .
.
(本小题满分12分)已知函数 .
.
(Ⅰ)若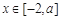 ,求
,求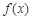 的值域;
的值域;
(Ⅱ)若存在实数t,当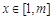 ,
, 恒成立,求实数
恒成立,求实数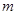 的取值范围.
的取值范围.