计算机执行右边的程序段后,输出的结果是
A. |
B. |
C. |
D. |
计算 的值为
的值为
A. |
B. |
C. |
D. |
以下给出的函数中,以 为周期的奇函数是
为周期的奇函数是
A. |
B. |
C. |
D. |
要从已编号( )的
)的 枚最新研制的某型导弹中随机抽取
枚最新研制的某型导弹中随机抽取 枚来进行发射试验,用系统抽样方法确定所选取的
枚来进行发射试验,用系统抽样方法确定所选取的 枚导弹的编号可能是
枚导弹的编号可能是
A. |
B. |
C. |
D. |
若向量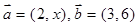 为共线向量,则
为共线向量,则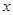 的值等于
的值等于
| A.2 | B.3 | C.4 | D.5 |
设一组数据的平均数是 ,方差是
,方差是 ,若将这组数据中的每一个数据都加上
,若将这组数据中的每一个数据都加上 ,得到一组新数据,则所得新数据的平均数和方差分别是
,得到一组新数据,则所得新数据的平均数和方差分别是
A.  |
B.  |
C.  |
D.  |
一只蚂蚁在三边长分别为3、4、5的三角形面上自由爬行,某时刻该蚂蚁距离三角形的三个顶点的距离不超过1的概率为
A. |
B. |
C. |
D. |
用秦九韶算法计算函数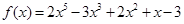 的值,
的值,
若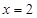 ,则
,则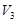 的值是
的值是
A.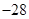 |
B.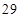 |
C.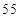 |
D. |
阅读如图所示的程序框图,运行相应的程序,则输出的 的值为
的值为
| A.-1 | B.1 | C.0 | D.3 |
已知向量 ,
,
则 的值为
的值为
A. |
B. |
C. |
D. |
四进制数  化为十进制数为 .
化为十进制数为 .
若 ,
, ,则
,则 的值是 .
的值是 .
函数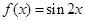 的图像可以由
的图像可以由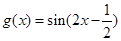 的图像向左平移 个单位得到.
的图像向左平移 个单位得到.
下列式子描述正确的有 .
① ;
;
② ;
;
③ ;
;
④ ;
;
⑤ ;
;
⑥ .
.
在平面斜坐标系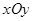 中,
中,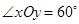 ,平面上任意一点
,平面上任意一点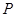 关于斜坐标系
关于斜坐标系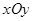 的斜坐标定义为:若
的斜坐标定义为:若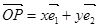 ,其中向量
,其中向量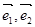 分别为斜坐标轴
分别为斜坐标轴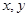 轴同方向的单位向量,则
轴同方向的单位向量,则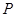 点的坐标为
点的坐标为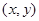 .
.
(1)若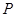 点的坐标为
点的坐标为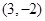 ,则
,则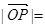 ;
;
(2)以 为圆心,2为半径的圆在斜坐标系下的方程为 .
为圆心,2为半径的圆在斜坐标系下的方程为 .
(本小题满分7分)已知 ,求下列式子的值.
,求下列式子的值.
(1)
(2)
(本小题满分7分)将一枚质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,记第一次出现的点数为 ,第二次出现的点数为
,第二次出现的点数为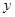 .
.
(Ⅰ)求事件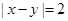 的概率;
的概率;
(Ⅱ)求事件“点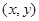 在圆
在圆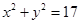 面上”(包括边界)的概率.
面上”(包括边界)的概率.
(本小题满分8分)从某校高一年级800名学生中随机抽取100名测量身高,测量后发现被抽取的学生身高全部介于155厘米和195厘米之间,将测量结果分为八组:第一组 ,第二组
,第二组 ,……,第八组
,……,第八组 ,得到频率分布直方图如右.
,得到频率分布直方图如右.
(Ⅰ)计算第七组[185,190)的样本数;并估计这个高一年级800名学生中身高在170厘米以下的人数;
(Ⅱ) 求出这100名学生身高的中位数、平均数.
(本小题满分8分)已知向量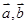 不共线,
不共线,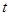 为实数.
为实数.
(Ⅰ)若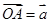 ,
,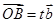 ,
,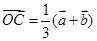 ,当
,当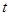 为何值时,
为何值时,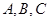 三点共线;
三点共线;
(Ⅱ)若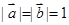 ,且
,且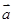 与
与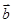 的夹角为
的夹角为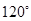 ,实数
,实数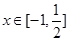 ,求
,求 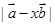 的取值范围.
的取值范围.
(本小题满分10分)如图所示,在 中,
中, ,若
,若 为
为 的外心.
的外心.
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的值;
的值;
(Ⅲ)若平面内一点 满足
满足




 ,试判定点
,试判定点 的位置.
的位置.
(本小题满分10分)已知函数 .
.
(Ⅰ)求 的最小正周期、对称轴和单调递增区间;
的最小正周期、对称轴和单调递增区间;
(Ⅱ)若函数 与
与 关于直线
关于直线 对称,求
对称,求 在闭区间
在闭区间 上的最大值和最小值.
上的最大值和最小值.