不等式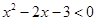 的解集是 .
的解集是 .
过两点 ,
, 的直线倾斜角是
的直线倾斜角是 ,则
,则 的值是 .
的值是 .
在等差数列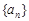 中,
中, ,
,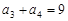 ,则
,则 .
.
已知,且 则的最小值为 .
则的最小值为 .
在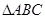 中,
中,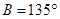 ,
, ,
, ,则此三角形的最大边长为 .
,则此三角形的最大边长为 .
圆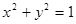 上的点到直线
上的点到直线 的距离的最小值是 .
的距离的最小值是 .
设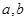 是两条不重合的直线,
是两条不重合的直线, 是两个不重合的平面,给出以下四个命题:
是两个不重合的平面,给出以下四个命题:
①若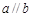 ,
,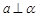 ,则
,则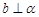 ;
;
②若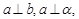 则
则 ;
;
③若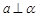 ,
, ,则
,则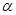 ∥
∥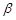 ;
;
④若 ,
,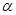

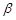 ,则
,则 ∥
∥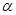 .
.
其中所有正确命题的序号是 .
已知等比数列的前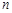 项和为
项和为 ,若
,若 ,则公比
,则公比 .
.
若变量满足,则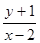 的取值范围是 .
的取值范围是 .
将一张坐标纸折叠一次,使点 与点
与点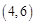 重合,且点
重合,且点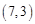 与点
与点 重合,则
重合,则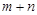 的值是 .
的值是 .
如图所示, 是空间四边形,
是空间四边形, 分别是四边上的点,并且
分别是四边上的点,并且 面
面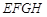 ,
, 面
面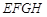 ,
,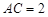 ,
,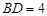 ,当
,当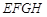 是菱形时,
是菱形时,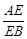 的值是 .
的值是 .
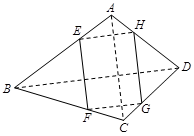
若关于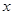 的不等式
的不等式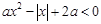 的解集为空集,则实数
的解集为空集,则实数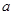 的取值范围是 .
的取值范围是 .
在平面直角坐标系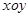 中,已知圆
中,已知圆 :
: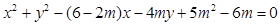 ,直线
,直线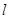 经过点
经过点 ,若对任意的实数
,若对任意的实数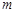 ,直线
,直线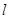 被圆
被圆 截得的弦长都是定值,则直线
截得的弦长都是定值,则直线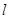 的方程为 .
的方程为 .
记数列 的前
的前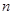 项和为
项和为 ,若不等式
,若不等式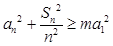 对任意等差数列
对任意等差数列 及任意正整数
及任意正整数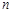 都成立,则实数
都成立,则实数 的最大值为 .
的最大值为 .
在中,角 的对边分别是,且.
的对边分别是,且.
(1)求角 的大小;
的大小;
(2)若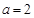 ,求面积的最大值.
,求面积的最大值.
如图,在四棱锥 中,四边形
中,四边形 是矩形,侧面
是矩形,侧面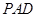 ⊥底面
⊥底面 ,若点
,若点 分别是
分别是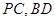 的中点.
的中点.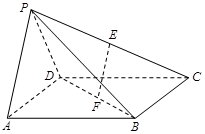
(1)求证: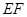 ∥平面
∥平面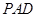 ;
;
(2)求证:平面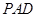 ⊥平面
⊥平面 .
.
已知的顶点 ,
, 边上的中线所在直线方程为,边上的高所在直线方程为.求
边上的中线所在直线方程为,边上的高所在直线方程为.求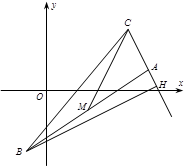
(1)顶点的坐标;
(2)直线的方程.
某工厂年初用49万元购买一台新设备,第一年设备维修及原料消耗的总费用6万元,以后每年都增加2万元,新设备每年可给工厂创造收益25万元.
(1)工厂第几年开始获利?
(2)若干年后,该工厂有两种处理该设备的方案:①年平均收益最大时,以14万元出售该设备;②总收益最大时,以9万元出售该设备.问出售该设备后,哪种方案年平均收益较大?
已知圆 :
: ,直线
,直线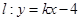 .
.
(1)若直线与圆 交于不同的两点
交于不同的两点 ,
, ,当=时,求的值.
,当=时,求的值.
(2)若 ,
, 是直线上的动点,过作圆
是直线上的动点,过作圆 的两条切线
的两条切线 、
、 ,切点为
,切点为 、
、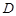 ,问:直线
,问:直线 是否过定点?若过定点,求出定点坐标;若不过定点,说明理由.
是否过定点?若过定点,求出定点坐标;若不过定点,说明理由.
(3)若 、
、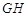 为圆
为圆 :
: 的两条相互垂直的弦,垂足为
的两条相互垂直的弦,垂足为 ,求四边形
,求四边形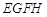 的面积的最大值.
的面积的最大值.
已知数列满足:,数列满足:,,数列的前项和为.
(1)求证:数列为等比数列;
(2)求证:数列为递增数列;
(3)若当且仅当时,取得最小值,求的取值范围.