如图,∠1+∠2=220°,b∥c,则∠3=( )

| A.110° | B.120° | C.70° | D.60° |
如图,AB∥CD,EF⊥AB于E,EF交CD于F,已知∠1=63°,则∠2=( )

| A.63° | B.53° | C.37° | D.27° |
下列各数2,π, ,﹣
,﹣ ,
, 中,无理数的个数是( )个.
中,无理数的个数是( )个.
| A.1 | B.2 | C.3 | D.4 |
点A(﹣2,1)是平面直角坐标系中的一点,则点A在( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
把点(2,﹣3)先向左平移3个单位长度,再向下平移2个单位长度得到的点的坐标是( )
| A.(﹣1,﹣5) | B.(5,﹣1) | C.(5,﹣5) | D.(﹣1,﹣1) |
方程组 的解为( )
的解为( )
A. |
B. |
C. |
D. |
扬州某中学2014-2015学年七年级一班40名同学第二次为四川灾区捐款,共捐款2000元,捐款情况如下表:
| 捐款(元) |
20 |
40 |
50 |
100 |
| 人数 |
10 |
|
|
8 |
表格中捐款40元和50元的人数不小心被墨水污染已看不清楚、若设捐款40元的有x名同学,捐款50元的有y名同学,根据题意,可得方程组( )
A.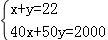 B.
B.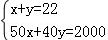
C. D.
D.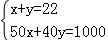
若x>y,则下列式子错误的是( )
| A.x﹣3>y﹣3 | B.3﹣x>3﹣y | C.﹣2x<﹣2y | D. > > |
在数轴上表示不等式x≥﹣2的解集,正确的是( )
A. |
B. |
C. |
D. |
某课外兴趣小组为了解所在地区的老年人的健康状况,分别作了四种不同的抽样调查,你认为抽样较合理的是( )
| A.在公园调查了1000名老年人的健康状况 |
| B.在医院调查了1000名老年人的健康状况 |
| C.调查了100名小区内老年邻居的健康状况 |
| D.利用派出所的户籍网随机调查了该地区10%的老年人的健康状况 |
9的算术平方根是 .
已知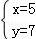 是方程kx﹣2y﹣1=0的解,则k的值为 .
是方程kx﹣2y﹣1=0的解,则k的值为 .
点(﹣3,6)到x轴的距离是 .
若点A(a+3,a﹣2)在y轴上,则点A的坐标为 .
如图,AD∥BC,∠D=100°,CA平分∠BCD,则∠DAC= 度.

如图,△ABC沿射线AC方向平移2cm得到△A′B′C′,若AC=3cm,则A′C= cm.

计算:5 ﹣3
﹣3 = .
= .
若关于x的不等式组 的解集是x>2,则m的取值范围是 .
的解集是x>2,则m的取值范围是 .
解方程组 .
.
解不等式组: ,并把它的解集在数轴上表示出来.
,并把它的解集在数轴上表示出来.
如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).

(1)写出点A、B的坐标:
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,则A′B′C′的三个顶点坐标分别是A′(,)、B′(,)、C′(,).
(3)△ABC的面积为 .
如图,EF⊥CD于F,GH⊥CD于H,已知∠1=70°,求∠3的度数.
如图,已知:DF∥AC,∠C=∠D.求证:BD∥CE.
将某雷达测速区监测到的一组汽车的时速数据整理,得到其频数分布表(未完成):
| 数据段 |
30~40 |
40~50 |
50~60 |
60~70 |
70~80 |
总计 |
| 频 数 |
10 |
40 |
|
|
20 |
|
| 百分比 |
5% |
|
40% |
|
10% |
|
注:30~40为时速大于等于30千米而小于40千米,其他类同.
(1)请你把表中的数据填写完整;
(2)补全频数分布直方图;
(3)如果此路段汽车时速超过60千米即为违章,则违章车辆共有多少辆?

一家服装店老板到厂家选购A、B两种型号的服装,若购进A种型号服装9件,B种型号服装10件,需要1810元;若购进A种型号服装12件,B种型号服装8件,需要1880元.问A、B两种型号的服装每件分别为多少元?