下列图形中，既是轴对称图形，又是中心对称图形是（ ）．
A． |
B． |
C． |
D． |
下列分式中是最简分式的是（ ）．
A． |
B． |
C． |
D． |
下列调查中，适合普查的是（ ）．
| A．中学生最喜欢的电视节目 |
| B．某张试卷上的印刷错误 |
| C．质检部门对各厂家生产的电池使用寿命的调查 |
| D．中学生上网情况 |
下列各式中，与
是同类二次根式的是（ ）．
A． |
B． |
C． |
D． |
在平面中，下列说法正确的是（ ）．
| A．四边相等的四边形是正方形 |
| B．四个角相等的四边形是矩形 |
| C．对角线相等的四边形是菱形 |
| D．对角线互相垂直的四边形是平行四边形 |
已知点P（x1，﹣2）、Q（x2，2）、R（x3，3）三点都在反比例函数y=
的图象上，则下列关系正确的是（ ）．
| A．x1＜x3＜x2 | B．x＜1x2＜x3 | C．x3＜x2＜x1 | D．x2＜x3＜x1 |
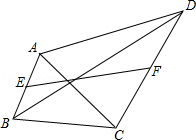
如图，菱形ABCD的边长为4，过点A、C作对角线AC的垂线，分别交CB和AD的延长线于点E、F，AE=3，则四边形AECF的周长为（ ）．
A．22 B．18 C．14 D．11
如图，由25个点构成的5×5的正方形点阵中，横纵方向相邻的两点之间的距离都是1个单位．定义：由点阵中四个点为顶点的平行四边形叫阵点平行四边形．图中以A，B为顶点，面积为2的阵点平行四边形的个数为（ ）．
| A．3 | B．6 | C．7 | D．9 |
在分式
中，当x= 时分式没有意义．
任意选择电视的某一频道，正在播放动画片，这个事件是 事件．（填“必然”“不可能”或“不确定”）
若x＜0，则
的结果是 ．
在一个不透明的口袋中装有若干个质地相同而颜色可能不全相同的球，如果口袋中装有3个黄球，且摸出黄球的概率为
，那么袋中共有 个球．
已知菱形的两条对角线长分别是6和8，则这个菱形的面积为 ．
已知
，则
的值是 ．
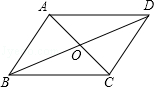
如图，▱ABCD的对角线相交于点O，BC=7cm，BD=10cm，AC=6cm，则△AOD的周长为 cm．
如图，矩形OBCD的顶点C的坐标为（1，3），则线段BD的长等于 ．
在四边形ABCD中，对角线AC⊥BD且AC=6、BD=8，E、F分别是边AB、CD的中点，则EF= ．
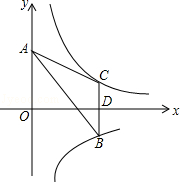
如图．两双曲线y=
与y=﹣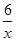
分别位于第一、第四象限，A是y轴上任意一点，B是y=﹣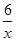上的点，C是y=上的点，线段BC⊥x轴于点D，且3BD=2CD，则△ABC的面积为 ．
（1）计算
；
（2）解方程：
．
先化简
，然后从1、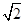
、﹣1中选取一个你认为合适的数作为a的值代入求值．
如图所示的正方形网格中，△ABC的顶点均在格点上，请在所给直角坐标系中按要求画图和解答下列问题：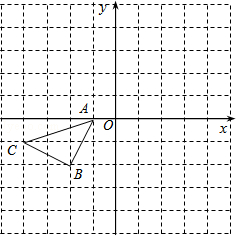
（1）以A点为旋转中心，将△ABC绕点A顺时针旋转90°得△AB1C1，画出△AB1C1．
（2）作出△ABC关于坐标原点O成中心对称的△A2B2C2．
2014年全国两会民生话题成为社会焦点．合肥市记者为了了解百姓“两会民生话题”的聚焦点，随机调查了合肥市部分市民，并对调查结果进行整理．绘制了如图所示的不完整的统计图表．
| 组别 |
焦点话题 |
频数（人数） |
| A |
食品安全 |
80 |
| B |
教育医疗 |
m |
| C |
就业养老 |
n |
| D |
生态环保 |
120 |
| E |
其他 |
60 |
请根据图表中提供的信息解答下列问题：
（1）填空：m= ，n= ．扇形统计图中E组所占的百分比为 %；
（2）合肥市人口现有750万人，请你估计其中关注D组话题的市民人数；
（3）若在这次接受调查的市民中，随机抽查一人，则此人关注C组话题的概率是多少？
已知如图，在菱形ABCD中，对角线AC、BD相交于点O，DE∥AC，AE∥BD．
（1）求证：四边形AODE是矩形；
（2）若AB=6，∠BCD=120°，求四边形AODE的面积．
如图，点B（3，3）在双曲线y=
（x＞0）上，点D在双曲线y=﹣
（x＜0）上，点A和点C分别在x轴、y轴的正半轴上，且点A、B、C构成的四边形为正方形．
（1）求k的值；
（2）求点A的坐标．
宜兴紧靠太湖，所产百合有“太湖人参”之美誉，今年百合上市后，甲、乙两超市分别用12000元以相同的进价购进质量相同的百合，甲超市销售方案是：将百合按分类包装销售，其中挑出优质的百合400千克，以进价的2倍价格销售，剩下的百合以高于进价10%销售．乙超市的销售方案是：不将百合分类，直接包装销售，价格按甲超市分类销售的两种百合售价的平均数定价．若两超市将百合全部售完，其中甲超市获利8400元（其它成本不计）．问：
（1）百合进价为每千克多少元？
（2）乙超市获利多少元？并比较哪种销售方式更合算．
如图1，直角梯形ABCD中，AD∥BC，∠ADC=90°，AD=8，BC=6，点M从点D出发，以每秒2个单位长度的速度向点A运动，同时，点N从点B出发，以每秒1个单位长度的速度向点C运动．其中一个动点到达终点时，另一个动点也随之停止运动．过点N作NP⊥AD于点P，连接AC交NP于点Q，连接MQ．设运动时间为t秒．
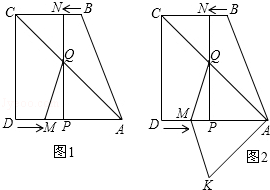
（1）AM= ，AP= ．（用含t的代数式表示）
（2）当四边形ANCP为平行四边形时，求t的值
（3）如图2，将△AQM沿AD翻折，得△AKM，是否存在某时刻t，
①使四边形AQMK为为菱形，若存在，求出t的值；若不存在，请说明理由
②使四边形AQMK为正方形，则AC= ．