已知各项均为正数的等比数列{ },
}, =5,
=5, =10,则
=10,则 =( )
=( )
A. |
B.7 | C.6 | D. |
若 为实数,则下列命题正确的是( )
为实数,则下列命题正确的是( )
A.若 ,则 ,则 |
B.若 ,则 ,则 |
C.若 ,则 ,则 |
D.若 ,则 ,则 |
已知直线 平行,则
平行,则 的值是( )
的值是( )
| A.0或1 | B.1或 |
C.0或 |
D. |
已知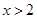 ,则函数
,则函数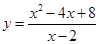 的最小值是( )
的最小值是( )
| A.5 | B.4 | C.8 | D.6 |
一个多面体的三视图如图所示,则该多面体的体积为( )

A. |
B.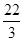 |
C.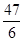 |
D.7 |
关于直线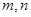 与平面
与平面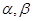 ,有以下四个命题:
,有以下四个命题:
①若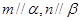 且
且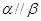 ,则
,则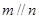 ;
;
②若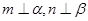 且
且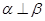 ,则
,则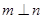 ;
;
③若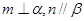 且
且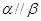 ,则
,则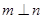 ;
;
④若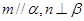 且
且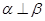 ,则
,则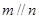 ;
;
其中正确命题的序号是( )
| A.①② | B.③④ | C.①④ | D.②③ |
在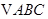 中,内角
中,内角 的对边分别是
的对边分别是 ,若
,若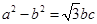 ,
,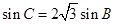 ,则
,则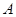 =( )
=( )
A.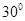 |
B.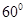 |
C. |
D. |
已知点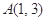 ,
, ,若直线
,若直线 :
: 与线段
与线段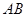 没有交点,则
没有交点,则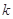 的取值范围是( )
的取值范围是( )
A.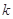 > > |
B.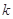 < < |
C.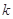 > > 或 或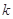 <-2 <-2 |
D.-2<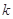 < < |
设等差数列 满足
满足 ,公差
,公差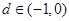 ,当且仅当
,当且仅当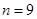 时,数列
时,数列 的前
的前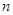 项和
项和 取得最大值,求该数列首项
取得最大值,求该数列首项 的取值范围( )
的取值范围( )
A.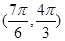 |
B. |
C.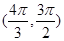 |
D.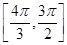 |
若正实数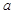 ,
, 满足
满足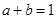 ,则( )
,则( )
A.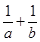 有最大值4 有最大值4 |
B. 有最小值 有最小值 |
C. 有最大值 有最大值 |
D.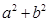 有最小值 有最小值 |
点 是不等式组
是不等式组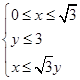 表示的平面区域
表示的平面区域 内的一动点,且不等式
内的一动点,且不等式
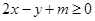 恒成立,则
恒成立,则 的取值范围是( )
的取值范围是( )
A.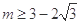 |
B.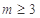 |
C.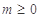 |
D.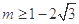 |
如图,正方体 的棱线长为1,线段
的棱线长为1,线段 上有两个动点
上有两个动点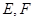 ,且
,且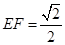 ,则下列结论中错误的是( )
,则下列结论中错误的是( )

A.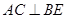 |
B.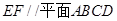 |
C.三棱锥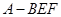 的体积为定值 的体积为定值 |
D.异面直线 所成的角为定值 所成的角为定值 |
经过点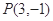 ,且在
,且在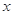 轴上的截距等于在
轴上的截距等于在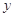 轴上的截距的
轴上的截距的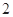 倍的直线
倍的直线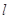 的方程是_____.
的方程是_____.
一个圆锥和一个半球有公共底面,如果圆锥的体积与半球的体积恰好相等,则圆锥轴截面顶角的余弦值是
 中角
中角 的对边分别为
的对边分别为 ,已知
,已知 若满足条件的三角形有两个,则
若满足条件的三角形有两个,则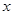 的取值范围是___________.
的取值范围是___________.
已知数列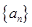 满足
满足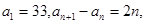 则
则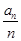 的最小值为__________.
的最小值为__________.
已知关于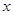 的不等式
的不等式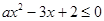 的解集为
的解集为 .
.
(1)求实数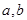 的值;
的值;
(2)解关于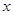 的不等式:
的不等式: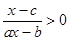 (
(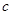 为常数).
为常数).
设公差不为0的等差数列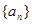 的首项为1,且
的首项为1,且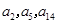 构成等比数列.
构成等比数列.
(Ⅰ)求数列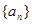 的通项公式;
的通项公式;
(Ⅱ)若数列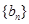 满足
满足 …
…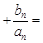 1-
1-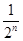 ,n∈N*,求
,n∈N*,求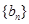 的前n项和
的前n项和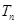 .
.
在△ 中,
中, 所对的边分别为
所对的边分别为 ,
, ,
, .
.
(1)求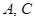 ;
;
(2)若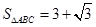 ,求
,求 .21世纪教育
.21世纪教育
已知直线方程为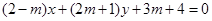 ,其中
,其中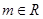
(1)求证:直线恒过定点;
(2)当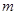 变化时,求点
变化时,求点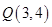 到直线的距离的最大值;
到直线的距离的最大值;
(3)若直线分别与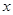 轴、
轴、 轴的负半轴交于
轴的负半轴交于 两点,求
两点,求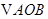 面积的最小值及此时的直线方程.
面积的最小值及此时的直线方程.
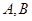 两仓库分别有编织袋50万个和30万个,由于抗洪抢险的需要,现需调运40万个到甲地,20万个到乙地.已知从
两仓库分别有编织袋50万个和30万个,由于抗洪抢险的需要,现需调运40万个到甲地,20万个到乙地.已知从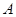 仓库调运到甲、乙两地的运费分别为120元/万个、180元/万个;从
仓库调运到甲、乙两地的运费分别为120元/万个、180元/万个;从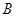 仓库调运到甲、乙两地的运费分别为100元/万个、150元/万个.问如何调运,能使总运费最小?总运费的最小值是多少?
仓库调运到甲、乙两地的运费分别为100元/万个、150元/万个.问如何调运,能使总运费最小?总运费的最小值是多少?
已知几何体 的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
(Ⅰ)求此几何体的体积 的大小;
的大小;
(Ⅱ)求异面直线DE与AB所成角的余弦值;
(Ⅲ)求二面角A-ED-B的正弦值.