直线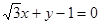 的倾斜角为
的倾斜角为
A.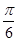 |
B.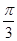 |
C.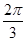 |
D.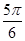 |
数列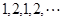 的通项公式不可能为
的通项公式不可能为
A.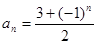 |
B.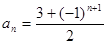 |
C.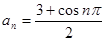 |
D.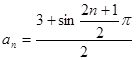 |
已知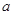 、
、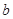 为非零实数,且
为非零实数,且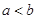 ,则下列不等式成立的是.
,则下列不等式成立的是.
A.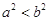 |
B.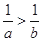 |
C.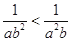 |
D.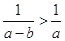 |
在各项都为正数的等比数列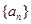 中,
中,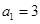 ,前三项的和为21,则
,前三项的和为21,则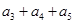 =
=
| A.33 | B.72 | C.84 | D.189 |
一个几何体的三视图如图所示,其中俯视图与左视图均为半径是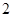 的圆,则这个几何体的体积是
的圆,则这个几何体的体积是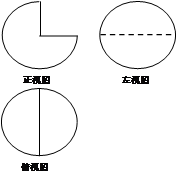
A. |
B.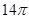 |
C.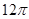 |
D.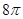 |
直线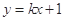 与圆
与圆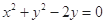 的位置关系是
的位置关系是
| A.相交 | B.相切 |
| C.相离 | D.取决于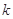 的值[ 的值[ |
若点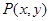 的坐标
的坐标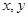 满足约束条件:
满足约束条件: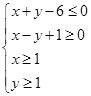 ,则
,则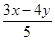 的最大值为
的最大值为
A.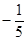 |
B. |
C.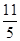 |
D.11 |
已知两个平面垂直,下列命题中:
(1)一个平面内已知直线必垂直于另一个平面内的任意一条直线;
(2)一个平面内已知直线必垂直于另一个平面内的无数条直线;
(3)一个平面内的任意一条直线必垂直于另一个平面;
(4)过一个平面内任意一点作交线的垂线,则此垂线必垂直于另一个平面.其中正确命题的个数有
| A.1 | B.2 | C.3 | D.4 |
在正方体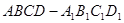 中,异面直线
中,异面直线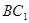 与
与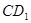 所成角的余弦值为
所成角的余弦值为
A.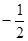 |
B.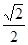 |
C.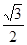 |
D.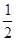 |
若点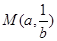 和
和 都在直线
都在直线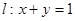 上,又点
上,又点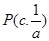 和点
和点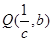 ,则
,则
A.点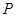 和 和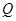 都不在直线 都不在直线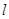 上 上 |
B.点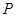 和 和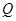 都在直线 都在直线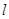 上 上 |
C.点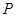 在直线 在直线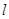 上且 上且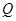 不在直线 不在直线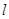 上 上 |
D.点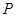 不在直线 不在直线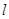 上且 上且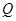 在直线 在直线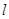 上 上 |
在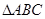 中,角
中,角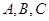 所对的边分别为
所对的边分别为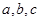 ,若
,若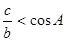 ,则
,则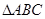 为.
为.
| A.钝角三角形 | B.直角三角形 | C.锐角三角形 | D.等边三角形 |
若数列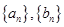 的通项公式分别是
的通项公式分别是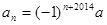 ,
,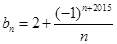 ,且
,且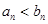 对任意
对任意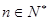 恒成立,则实数
恒成立,则实数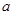 的取值范围是
的取值范围是
A.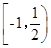 |
B. |
C.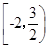 |
D.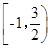 |
不等式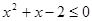 的解集为_______________.
的解集为_______________.
已知等差数列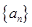 ,满足
,满足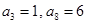 ,则此数列的前
,则此数列的前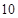 项的和
项的和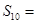 .
.
直线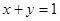 与直线
与直线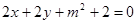 间距离的最小值为___________.
间距离的最小值为___________.
在正四面体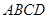 中,有如下四个命题:
中,有如下四个命题:
①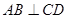 ;
;
②该四面体外接球的半径与内切球半径之比为 ;
;
③分别取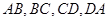 的中点
的中点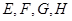 并顺次连结所得四边形是正方形;
并顺次连结所得四边形是正方形;
④三组对棱中点的连线段交于一点并被该点平分.
则其中为真命题的序号为__________________.(填上你认为是真命题的所有序号).
已知点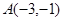 和点
和点 .
.
(Ⅰ)求过点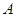 且与直线
且与直线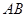 垂直的直线
垂直的直线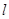 的一般式方程;
的一般式方程;
(Ⅱ)求以线段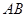 为直径的圆
为直径的圆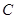 的标准方程.
的标准方程.
在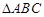 中,角
中,角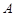 、
、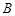 、
、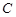 对的边分别为
对的边分别为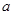 、
、 、
、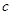 ,且
,且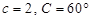
(Ⅰ)求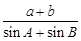 的值;
的值;
(Ⅱ)若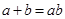 ,求
,求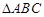 的面积
的面积 .
.
已知直线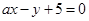 与圆
与圆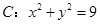 相交于不同两点
相交于不同两点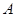 ,
,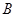 .
.
(Ⅰ)求实数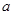 的取值范围
的取值范围
(Ⅱ)是否存在实数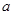 ,使得过点
,使得过点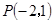 的直线
的直线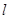 垂直平分弦
垂直平分弦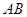 ?若存在,求出
?若存在,求出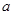 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
某小区内有如图所示的一矩形花坛,现将这一矩形花坛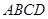 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛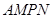 ,要求
,要求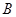 点在
点在 上,
上,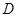 点在
点在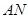 上,且对角线
上,且对角线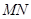 过
过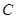 点,已知
点,已知 米,
米,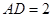 米.
米.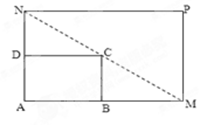
(Ⅰ)要使矩形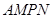 的面积大于32平方米,则
的面积大于32平方米,则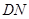 的长应在什么范围内?
的长应在什么范围内?
(Ⅱ)当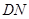 的长度是多少时,矩形花坛
的长度是多少时,矩形花坛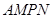 的面积最小?并求出最小值.
的面积最小?并求出最小值.
某家居装饰设计的形状是如图所示的直三棱柱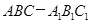 ,其中,
,其中,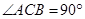 ,
,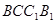 是边长为2(单位:米)的正方形,
是边长为2(单位:米)的正方形,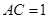 ,点
,点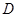 为棱
为棱 上的动点.
上的动点.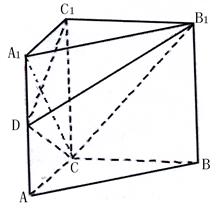
(Ⅰ)现需要对该装饰品的表面进行涂漆处理,假设每平方米的油漆费是40元,则需油漆费多少元?(提示: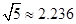 ,结果保留到整数位)
,结果保留到整数位)
(Ⅱ)当点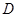 为何位置时,
为何位置时,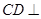 平面
平面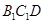 ?
?
已知等差数列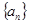 的公差为
的公差为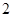 ,且
,且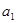 ,
,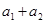 ,
,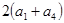 成等比数列.
成等比数列.
(Ⅰ)求数列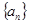 的通项公式;
的通项公式;
(Ⅱ)设数列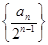 的前
的前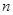 学科王项和为
学科王项和为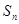 ,求证:
,求证: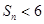 .
.