已知向量 ,
, ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
一段圆弧的长度等于其圆内接正方形的边长,则其圆心角的弧度数为( )
A. |
B. |
C. |
D. |
在 中,已知
中,已知  ,那么
,那么 一定是( )
一定是( )
| A.直角三角形 | B.等腰直角三角形 |
| C.等腰三角形 | D.正三角形 |
 的值等于( )
的值等于( )
A. |
B. |
C. |
D.  |
为了得到函数 的图像,可以将函数
的图像,可以将函数 的图像( )
的图像( )
A.向右平移 个单位长度 个单位长度 |
B.向右平移 个单位长度 个单位长度 |
C.向左平移 个单位长度 个单位长度 |
D.向左平移 个单位长度 个单位长度 |
已知点 在第一象限,则在
在第一象限,则在 内
内 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
函数 的部分图象如图所示.则
的部分图象如图所示.则 ( )
( )

A. |
B. |
C. |
D. |
设  ,
, ,
, 则有( )
则有( )
A. |
B. |
C. |
D. |
 值域为( )
值域为( )
A. |
B. |
C. |
D. |
如图所示, 、
、 为
为 内的两点,且
内的两点,且 ,
,  =
=


 ,则
,则 的面积与
的面积与 的面积之比为( )
的面积之比为( )

A. |
B. |
C. |
D. |
已知向量 ,
, ,
, 与
与 的夹角为
的夹角为 ,则
,则 .
.
已知角 的顶点在坐标原点,始边与
的顶点在坐标原点,始边与 轴正半轴重合终边在直线
轴正半轴重合终边在直线 上,则
上,则  .
.
如图,在正方形 中,
中, ,点
,点 为
为 的中点,点
的中点,点 在边
在边 上.若
上.若 ,则
,则 .
.

已知函数 ,给出下列四个说法:
,给出下列四个说法:
① 为奇函数;
为奇函数;
② 的一条对称轴为
的一条对称轴为 ;
;
③ 的最小正周期为
的最小正周期为 ;
;
④ 在区间
在区间 上单调递增;
上单调递增;
⑤ 的图象关于点
的图象关于点 成中心对称.
成中心对称.
其中正确说法的序号是 .
已知 、
、 、
、 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中 .
.
(1)若 ,且
,且 //
// ,求
,求 的坐标;
的坐标;
(2)若 ,且
,且 与
与 垂直,求
垂直,求 与
与 的夹角
的夹角 .
.
16.(本小题满分12分)
已知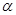 为第三象限角,且
为第三象限角,且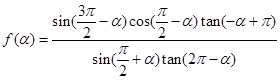 .
.
(1) 化简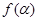 ;
;
(2) 若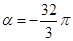 ,求
,求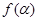 的值.
的值.
(3) 若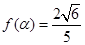 ,求
,求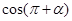 的值.
的值.
已知  均为锐角,且
均为锐角,且 ,
, .
.
(1)求 的值;
的值;
(2)求 的值.
的值.
已知函数 为奇函数,且
为奇函数,且 ,其中
,其中 ,
, .
.
(1) 求 ,
, 的值;[
的值;[
(2) 令  ,
, ,求
,求 的最值并求出相应的
的最值并求出相应的 的值.
的值.
已知向量 ,
, ,且
,且 .
.
(1)求 及
及 ;
;
(2)若 的最小值为
的最小值为 ,求实数
,求实数 的值.
的值.
已知 为
为 的外心,以线段
的外心,以线段 为邻边作平行四边形,第四个顶点为
为邻边作平行四边形,第四个顶点为 ,再以
,再以 为邻边作平行四边形,它的第四个顶点为
为邻边作平行四边形,它的第四个顶点为 .
.
(1)若 ,试用
,试用 、
、 、
、 表示
表示 ;
;
(2)证明: ;
;
(3)若 的
的 ,
, ,外接圆的半径为
,外接圆的半径为 ,用
,用 表示
表示 .
.