设全集 集合
集合 集合
集合 ,则
,则 =
=
A. |
B. |
C. |
D. |
设 ,则使函数
,则使函数 的定义域为R且为奇函数的所有
的定义域为R且为奇函数的所有 的值有
的值有
| A.1个 | B.2个 | C.3个 | D.4个 |
函数 的零点个数为
的零点个数为
| A.3 | B.2 | C.1 | D.0 |
函数 在区间A上是增函数,则区间A是
在区间A上是增函数,则区间A是
A. |
B. |
C. |
D. |
已知点A(1,1),B(3,3),则线段AB的垂直平分线的方程是
A. |
B.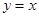 |
C.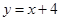 |
D. |
棱长都是 的三棱锥的表面积为
的三棱锥的表面积为
A. |
B.2 |
C.3 |
D.4 |
△ABC中,点A(4,-1),AB的中点为M(3,2),重心为P(4,2),则边BC的长为
| A.10 | B.8 | C.5 | D.5 |
如果两条直线l1: 与l2:
与l2: 平行,那么a等
平行,那么a等
| A.1 | B.-1 | C.2 | D. |
正方体的棱长和外接球的半径之比为
A. ∶1 ∶1 |
B. ∶2 ∶2 |
C.2∶ |
D. ∶3 ∶3 |
若 、
、 、
、 是互不相同的空间直线,
是互不相同的空间直线, 、
、 是不重合的平面,则下列结论正确的是
是不重合的平面,则下列结论正确的是
A.   |
B.   |
C.   |
D.   |
若某几何体的三视图(单位:cm)如图所示,则此几何体的体积

A. |
B. |
C. |
D. |
对于 ,给出下列四个不等式
,给出下列四个不等式
① ;
;
② ;
;
③ ;
;
④ .
.
其中成立的是
| A.①与③ | B.①与④ | C.②与③ | D.②与④ |
已知 ;
; ;
; .则
.则 的大小关系是(从大到小排列)__________.
的大小关系是(从大到小排列)__________.
已知方程2x=10-x的根x∈(k,k+1),k∈Z,则k =________.
已知 为奇函数,且
为奇函数,且 时,
时, ,则
,则 .
.
对于函数f(x)=x|x|+px+q,现给出四个结论:
①q=0时,f(x)为奇函数;
②y=f(x)的图象关于(0,q)对称;
③p=0,q>0时,方程f(x)=0有且只有一个实数根;
④方程f(x)=0至多有两个实数根.
其中正确的结论的序号为________.
(本小题满分10分)不用计算器求下列各式的值.
(Ⅰ) ;
;
(Ⅱ)设 ,求
,求 .
.
(本小题满分12分)已知二次函数 ,当
,当 时函数取最小值
时函数取最小值 ,且
,且 .
.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)若 在区间
在区间 上不单调,求实数
上不单调,求实数 的取值范围.
的取值范围.
(本小题满分12分)如图,空间四边形 的对棱
的对棱 、
、 成
成 的角,且
的角,且 ,平行于
,平行于 与
与 的截面分别交
的截面分别交 、
、 、
、 、
、 于
于 、
、 、
、 、
、 .
.
(Ⅰ)求证:四边形 为平行四边形;
为平行四边形;
(Ⅱ) 在
在 的何处时截面
的何处时截面 的面积最大?最大面积是多少?
的面积最大?最大面积是多少?
(本小题满分12分)已知函数

(Ⅰ)求函数 的定义域;
的定义域;
(Ⅱ)求函数 的零点;
的零点;
(Ⅲ)若函数 的最小值为-4,求
的最小值为-4,求 的值.
的值.
(本小题满分12分)如图,棱长为1的正方体ABCD-A1B1C1D1中,
(Ⅰ)求证:AC⊥平面B1D1DB;
(Ⅱ)求证:BD1⊥平面ACB1;
(Ⅲ)求三棱锥B-ACB1体积.
(本小题满分12分)已知函数 -
- .
.
(Ⅰ)证明 是奇函数;
是奇函数;
(Ⅱ)判断 的单调性,并用定义证明;
的单调性,并用定义证明;
(Ⅲ)求 在[-1,2] 上的最值.
在[-1,2] 上的最值.