下列命题正确的是( )
A.若 · · = = · · ,则 ,则 = = |
B.若 ,则 ,则 · · =0 =0 |
C.若 // // , , // // ,则 ,则 // // |
D.若 与 与 是单位向量,则 是单位向量,则 · · =1 =1 |
函数 的图象的一条对称轴是( )
的图象的一条对称轴是( )
A. |
B. |
C. |
D. |
已知角 的终边过点
的终边过点 ,
, ,则
,则 的值是( )
的值是( )
| A.1或-1 | B. 或 或 |
C.1或 |
D.-1或 |
已知 ,
, ,
, ,则
,则 等于( )
等于( )
A. |
B. |
C. |
D. |
计算下列几个式子,① ,②2(sin35°cos25°+sin55°cos65°), ③
,②2(sin35°cos25°+sin55°cos65°), ③ , ④
, ④  ,结果为
,结果为 的是( )
的是( )
| A.①② | B.①③ | C.①②③ | D.①②③④ |
函数y=cos( -2x)的单调递增区间是( )
-2x)的单调递增区间是( )
A.[kπ+ ,kπ+ ,kπ+ π] π] |
B.[kπ- π,kπ+ π,kπ+ ] ] |
C.[2kπ+ ,2kπ+ ,2kπ+ π] π] |
D.[2kπ- π,2kπ+ π,2kπ+ ](以上k∈Z) ](以上k∈Z) |
将函数 的图像左移
的图像左移 ,再将图像上各点横坐标压缩到原来的
,再将图像上各点横坐标压缩到原来的 ,则所得到的图象的解析式为( )
,则所得到的图象的解析式为( )
A. |
B. |
C. |
D. |
若 ,函数
,函数 在
在 上递增,则( )
上递增,则( )
A. |
B. |
C. |
D. |
O为平面上的定点,A、B、C是平面上不共线的三点,若( ―
― )·(
)·( +
+ ―2
―2 )=0,则DABC是( )
)=0,则DABC是( )
A.以AB为底边的等腰三角形
B.以BC为底边的等腰三角形
C.以AB为斜边的直角三角形
D.以BC为斜边的直角三角形
设平面向量 =(-2,1),
=(-2,1), =(λ,-1),若
=(λ,-1),若 与
与 的夹角为钝角,则λ的取值范围是( )
的夹角为钝角,则λ的取值范围是( )
A. |
B. |
C. |
D. |
若
 ,
, ,则tan
,则tan 等于( )
等于( )
A. |
B. 或 或 |
C. |
D. |
在△ABC中,若 ,则角B的值为( )
,则角B的值为( )
A. |
B. |
C. 或 或 |
D. 或 或 |
若平面向量 、
、 、
、 两两所成的角相等,且︱
两两所成的角相等,且︱ ︱=1,︱
︱=1,︱ ︱=1,︱
︱=1,︱ ︱=3,则︱
︱=3,则︱ +
+ +
+ ︱=_______________.
︱=_______________.
设 ,则
,则 =_____________.
=_____________.
关于x的方程 (0≤x≤
(0≤x≤ )有两相异根,则实数
)有两相异根,则实数 的取值范围是__________.
的取值范围是__________.
给出下列四个命题:
①函数y=sin(cosx)的最小正周期是 ;
;
②在△ABC中, 若AB=2,AC=3,∠ABC= ,则△ABC必为锐角三角形;
,则△ABC必为锐角三角形;
③函数 的值域是
的值域是 ;
;
④在同一坐标系中,函数 的图象和函数
的图象和函数 的图象有三个公共点;
的图象有三个公共点;
其中正确命题的是 (把你认为正确的序号都填上)
已知 =2,求值:
=2,求值:
(1) ;
;
(2) .
.
(本小题12分)已知sin(2α-β)=  ,sinβ=" -"
,sinβ=" -"  ,且α∈(
,且α∈( ,π),β∈(-
,π),β∈(- ,0),求sinα的值.
,0),求sinα的值.
(本小题满分12分)在 中,已知点
中,已知点 为线段
为线段 上的一点,且
上的一点,且 .
.
(1)试用 表示
表示 ;
;
(2)若 ,且
,且 ,求
,求 的值.
的值.
(本小题满分12分)(如图,某海滨浴场的岸边可近似地看成直线,位于岸边A处的救生员发现海中B处有人求救,救生员没有直接从A处游向B处,而是沿岸边自A跑到距离B最近的D处,然后游向B处,若救生员在岸边的行进速度为6米/秒,在海中的行进速度为2米/秒, 。
。
(1)分析救生员的选择是否正确;
(2)在AD上找一点C,使救生员从A到B的时间为最短,并求出最短时间。
(本小题13分)已知函数 的一系列对应值如下表:
的一系列对应值如下表:
 |
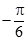 |
 |
 |
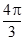 |
 |
 |
 |
 |
 |
|
 |
|
 |
|
 |
(1)根据表格提供的数据求函数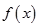 的解析式;
的解析式;
(2)求函数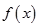 的单调递增区间和对称中心;
的单调递增区间和对称中心;
(3)若当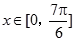 时,方程
时,方程 恰有两个不同的解,求实数
恰有两个不同的解,求实数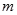 的取值范围.
的取值范围.
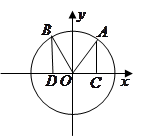
(本小题满分13分)如图,在平面直角坐标系 中,点
中,点 在单位圆
在单位圆 上,
上,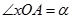 ,且
,且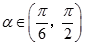 .
.
(1)若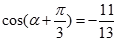 ,求
,求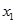 的值;
的值;
(2)若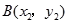 也是单位圆
也是单位圆 上的点,且
上的点,且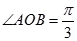 .过点
.过点 分别做
分别做 轴的垂线,垂足为
轴的垂线,垂足为 ,记
,记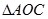 的面积为
的面积为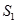 ,
, 的面积为
的面积为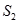 .设
.设 ,求函数
,求函数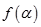 的最大值.
的最大值.