等比数列 中,
中, ,则
,则
| A.20 | B.16 | C.15 | D.10 |
如果 且
且 ,那么下列不等式中不一定成立的是
,那么下列不等式中不一定成立的是
A. |
B. |
C. |
D. |
在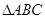 中,若
中,若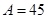 °,
°, °,
°, .则
.则 =
=
A.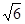 |
B.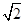 |
C.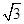 |
D.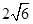 |
下列事件是随机事件的是
(1)连续两次掷一枚硬币,两次都出现正面向上.
(2)异性电荷相互吸引
(3)在标准大气压下,水在 ℃时结冰
℃时结冰
(4)任意掷一枚骰子朝上的点数是偶数
| A.(1)(2) | B.(2)(3) | C.(3)(4) | D.(1)(4) |
 中,
中, 则
则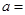
A. |
B. |
C.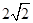 |
D. |
变量 满足
满足 ,目标函数
,目标函数 ,则
,则 的最小值是
的最小值是
A. |
B. |
C. |
D. |
已知等差数列 的公差为2,若
的公差为2,若 成等比数列,则
成等比数列,则
A. |
B. |
C. |
D. |
执行如图所示的程序框图,若输出的S=88,则判断框内应填入的条件是
A. |
B. |
C. |
D. |
甲、乙两名选手参加歌手大赛时,5名评委打的分数用茎叶图表示(如下图), 分别表示甲、乙选手的标准差,则
分别表示甲、乙选手的标准差,则 与
与 的关系是
的关系是
A. |
B. |
C. |
D.不能确定 |
在数列 中,
中, ,则数列
,则数列 的前n项和
的前n项和 的最大值是
的最大值是
| A.136 | B.140 | C.144 | D.148 |
下列说法正确的是
A.函数 的最小值为 的最小值为 |
B.函数 的最小值为 的最小值为 |
C.函数 的最小值为 的最小值为 |
D.函数 的最小值为 的最小值为 |
在钝角三角形 中,若
中,若 °,
°, ,则边长
,则边长 的取值范围是
的取值范围是
A. |
B. |
C. |
D. |
不等式 的解集是 .
的解集是 .
程序:M=1 M=M+1 M=M+2 PRINT M END M的最后输出值为 .
课题组进行城市空气质量调查,按地域把24个城市分成甲、乙、丙三组,对应的城市数分别为4,12,8.若用分层抽样从中抽取6个城市,则丙组中应抽取的城市数为________.
函数 的图象恒过定点
的图象恒过定点 ,若点
,若点 在直线
在直线 上,其中
上,其中 ,则
,则 的最小值为 .
的最小值为 .
(本小题满分12分)在等差数列 中,
中,
(Ⅰ)求通项 ;
;
(Ⅱ)求此数列前30项的绝对值的和.
(本小题满分12分)设 的内角
的内角 所对应的边长分别是
所对应的边长分别是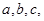 且
且
(Ⅰ)当 时,求
时,求 的值;
的值;
(Ⅱ)当 的面积为3时,求
的面积为3时,求 的值.
的值.
(本小题满分12分)某制造商3月生产了一批乒乓球,从中随机抽样100个进行检查,测得每个球的直径(单位:mm),将数据分组如下:
| 分组 |
频数 |
频率 |
| [39.95,39.97) |
10 |
|
| [39. 97,39.99) |
20 |
|
| [39.99,40.01) |
50 |
|
| [40.01,40.03] |
20 |
|
| 合计 |
100 |
|

(Ⅰ)请在上表中补充完成频率分布表(结果保留两位小数),并在图中画出频率分布直方图;
(Ⅱ)若以上述频率作为概率,已知标准乒乓球的直径为40.00 mm,试求这批球的直径误差不超过0.03 mm的概率;
(Ⅲ)统计方法中,同一组数据经常用该组区间的中点值(例如区间[39.99,40.01)的中点值是40.00作为代表.据此估计这批乒乓球直径的平均值(结果保留两位小数).
(本小题满分12分)已知 .
.
(Ⅰ)当 时,解不等式
时,解不等式 ;
;
(Ⅱ)若 ,解关于x的不等式
,解关于x的不等式 .
.
(本小题满分12分)设 的内角
的内角 所对的边分别为
所对的边分别为 且
且 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若 ,求
,求 的周长
的周长 的取值范围.
的取值范围.
已知数列 和
和 中,数列
中,数列 的前
的前 项和为
项和为 若点
若点 在函数
在函数 的图象上,点
的图象上,点 在函数
在函数 的图象上.设数列
的图象上.设数列
 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)求数列 的前
的前 项和
项和 ;
;
(Ⅲ)求数列 的最大值.
的最大值.