一个多边形的内角和为360°，则这个多边形是（ ）
| A．三角形 | B．四边形 | C．五边形 | D．六边形 |
某红外线波长为0.00 000 094m，用科学记数法把0.00 000 094m可以写成（ ）
A． m |
B． m |
C． m |
D． m |
下列运算正确的是（ ）
A． |
B． |
C． |
D． |
下列等式从左到右的变形，属于因式分解的是（ ）
| A．a（x－y）＝ax－ay | B．x2－1＝（x+1）（x－1） |
| C．（x+1）（x+3）＝x2+4x+3 | D．x2+2x+1＝x（x+2）+1 |
把不等式组
的解集在数轴上表示正确的是（ ）
若
，则实数m的值（ ）
A． |
B． |
C．1 | D．5 |
李明同学早上骑自行车上学，中途因道路施工需步行一段路，到学校共用时15分钟．他骑自行车的速度是250米/分钟，步行的速度是80米/分钟．他家离学校的距离是2900米．若他骑车和步行的时间分别为x分钟和y分钟，则列出的方程组是（ ）
A． |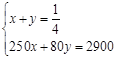
B． |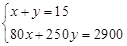
C． |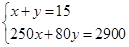
D． |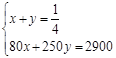
如图，大正方形的边长为m，小正方形的边长为n，若用x、y表示四个相同长方形的两边长（x＞y），给出以下关系式：①x+y＝m；②x－y＝n；③ xy＝． 其中正确的关系式的个数有（ ）
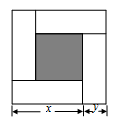
| A．0个 | B．1个 |
| C．2个 | D．3个 |
不等式
的解集是 .
将多项式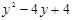
分解因式得 ．
若
，则用含x的代数式表示y为 ．
若
=3，则
的值是 ．
若命题“对于任意实数
，
的值都是正数”是假命题，则其中一个反例是
= .
已知
，y=3是二元一次方程
的一个解，则
.
若
，则
的值为 .
如图，有一块含有60°角的直角三角板的两个顶点放在矩形的对边上．如果∠1=15°，那么∠2的度数是 ．
已知不等式组
有解，则实数
的取值范围是 ．
若一个三角形的3边长分别是
cm、
cm、
cm，则的取值范围是 ．
计算：
．
先化简，再求值：
，其中
，
．
解不等式组
，并写出它的所有整数解．
如图，每个小正方形的边长为1个单位，每个小方格的顶点叫格点.
（1）画出△ABC向右平移4个单位后得到的△A1B1C1；
（2）画出△ABC的AB边上的中线CD，并求△BCD的面积.
已知x＋y＝3，且（x＋2）（y＋2）＝12．
（1）求xy的值； （2）求x2＋3xy＋y2的值．
已知，如图，DE∥BC，∠A=60°，∠B=50°；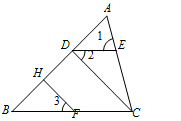
（1）求∠1的度数；
（2）若FH⊥AB于点H，且∠2=∠3，试判断CD与AB的位置关系？并加以证明．
某校准备组织七年级400名学生参加北京夏令营，已知用3辆小客车和1辆大客车每次可运送学生105人；用1辆小客车和2辆大客车每次可运送学生110人；
（1）每辆小客车和每辆大客车各能坐多少名学生？
（2）若学校计划租用小客车x辆，大客车y辆，一次送完，且恰好每辆车都坐满；
①请你设计出所有的租车方案；
②若小客车每辆需租金4000元，大客车每辆需租金7600元，请选出最省钱的租车方案，并求出最少租金．
如图，点C在∠MAN的边AM上，CD⊥AN，垂足为点D，点B在边AN上运动，∠BCA的平分线交AN于点E。
（1）若∠A＝30°，∠B＝70°，求∠ECD的度数；
（2）若∠A＝
，∠B＝
，求∠ECD的度数（用含
的式子表示）．