在复平面内,复数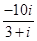 对应的点的坐标为()
对应的点的坐标为()
| A.(3,﹣1) | B.(1,﹣3) | C.(﹣1,﹣3) | D.(﹣3,﹣1) |
用反证法证明“若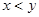 ,则
,则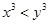 ”时,假设内容是()
”时,假设内容是()
A. |
B.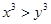 |
C. 或 或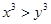 |
D. 或 或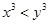 |
设随机变量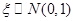 ,若
,若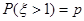 ,则
,则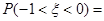 ( )
( )
A.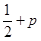 |
B.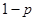 |
C.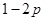 |
D.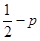 |
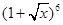 的展开式中有理项系数之和为( )
的展开式中有理项系数之和为( )
| A.64 | B.32 | C.24 | D.16 |
有3位同学参加测试,假设每位同学能通过测试的概率都是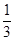 ,且各人能否通过测试是相互独立的,则至少有一位同学能通过测试的概率为( )
,且各人能否通过测试是相互独立的,则至少有一位同学能通过测试的概率为( )
A.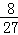 |
B.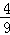 |
C.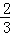 |
D.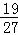 |
若离散型随机变量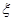 的分布列为:则随机变量
的分布列为:则随机变量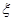 的期望为()
的期望为()
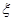 |
0 |
1 |
2 |
3 |
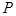 |
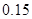 |
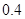 |
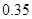 |
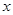 |
A.1.4 B.0.15 C.1.5 D.0.14
已知函数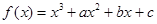 ,下列结论中错误的是()
,下列结论中错误的是()
A.若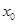 是 是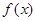 的极小值点,则 的极小值点,则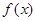 在区间 在区间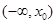 单调递减 单调递减 |
B.函数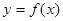 的图象是中心对称图形 的图象是中心对称图形 |
C.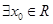 , ,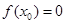 |
D.若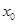 是 是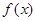 的极值点,则 的极值点,则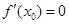 |
现有2门不同的考试要安排在5天之内进行,每天最多进行一门考试,且不能连续两天有考试,那么不同的考试安排方案种数有()
| A.6 | B.8 | C.12 | D.16 |
正方体ABCD﹣A1B1C1D1的棱长为1,M是棱AB的中点,点P是平面ABCD上的动点,P到直线A1D1的距离为d,且d2﹣|PM|2=1,则动点P的轨迹是()
| A.圆 | B.抛物线 | C.椭圆 | D.双曲线 |
现有男、女学生共8人,从男生中选2人,从女生中选1人分别参加数学、物理、化学三科竞赛,共有90种不同方案,那么男、女生人数分别是()
| A.男生2人,女生6人 | B.男生3人,女生5人 |
| C.男生5人,女生3人 | D.男生6人,女生2人 |
设双曲线 (
(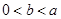 )的半焦距为
)的半焦距为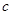 ,
,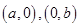 为直线
为直线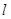 上两点,已知原点到直线
上两点,已知原点到直线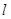 的距离为
的距离为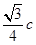 ,则双曲线的离心率为()
,则双曲线的离心率为()
A.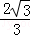 |
B.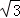 或2 或2 |
C.2或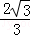 |
D.2 |
已知定义在 上的单调函数
上的单调函数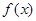 ,对
,对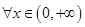 ,都有
,都有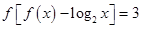 ,则方程
,则方程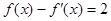 的解所在的区间是( )
的解所在的区间是( )
A.(0, ) ) |
B.(1,2) | C.( ,1) ,1) |
D.(2,3) |
复数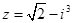 的共轭复数为 .
的共轭复数为 .
三位同学参加跳高、跳远、铅球项目的比赛,若每人都选择其中两个项目,则有且仅有两人选择的项目完全相同的概率是 (结果用最简分数表示).
已知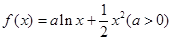 ,若对任意两个不等的正实数
,若对任意两个不等的正实数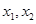 都有
都有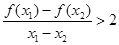 恒成立,则
恒成立,则 的取值范围是 .
的取值范围是 .
方程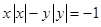 的曲线即为函数
的曲线即为函数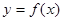 的图象,对于函数
的图象,对于函数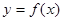 ,有如下结论:
,有如下结论:
①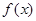 在R上单调递减;
在R上单调递减;
②函数 存在3个零点;
存在3个零点;
③函数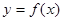 的值域是R;
的值域是R;
④函数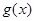 和
和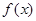 的图象关于原点对称,则函数
的图象关于原点对称,则函数 的图象就是方程
的图象就是方程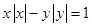 确定的曲线.
确定的曲线.
其中所有正确的命题序号是 .
已知书架中甲层有英语书2本和数学书3本,乙层有英语书1本和数学书4本.现从甲、乙两层中各取两本书.
(1)求取出的4本书都是数学书的概率.
(2)求取出的4本书中恰好有1本是英语书的概率.
已知函数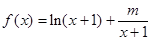 .
.
(1)当函数 在点
在点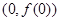 处的切线与直线
处的切线与直线 垂直时,求实数
垂直时,求实数 的值;
的值;
(2)若 时,
时,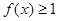 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知平面内一动点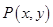 (
(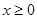 )到点
)到点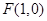 的距离与点
的距离与点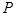 到
到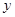 轴的距离的差等于1,
轴的距离的差等于1,
(1)求动点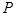 的轨迹
的轨迹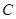 的方程;
的方程;
(2)过点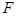 的直线
的直线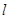 与轨迹
与轨迹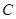 相交于不同于坐标原点
相交于不同于坐标原点 的两点
的两点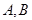 ,求
,求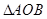 面积的最小值.
面积的最小值.
某理科考生参加自主招生面试,从7道题中(4道理科题3道文科题)不放回地依次任取3道作答.
(1)求该考生在第一次抽到理科题的条件下,第二次和第三次均抽到文科题的概率;
(2)规定理科考生需作答两道理科题和一道文科题,该考生答对理科题的概率均为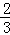 ,答对文科题的概率均为
,答对文科题的概率均为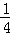 ,若每题答对得10分,否则得零分.现该生已抽到三道题(两理一文),求其所得总分
,若每题答对得10分,否则得零分.现该生已抽到三道题(两理一文),求其所得总分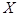 的分布列与数学期望
的分布列与数学期望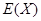 .
.
已知椭圆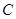 的中心在原点,焦点在
的中心在原点,焦点在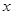 轴上,离心率为
轴上,离心率为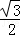 ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线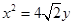 的焦点.
的焦点.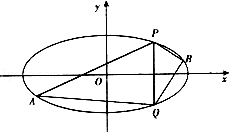
(I)求椭圆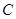 的方程;
的方程;
(II)直线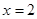 与椭圆交于
与椭圆交于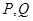 两点,
两点,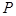 点位于第一象限,
点位于第一象限,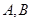 是椭圆上位于直线
是椭圆上位于直线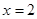 两侧的动点.
两侧的动点.
(i)若直线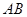 的斜率为
的斜率为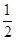 ,求四边形
,求四边形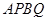 面积的最大值;
面积的最大值;
(ii)当点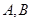 运动时,满足
运动时,满足 ,问直线
,问直线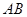 的斜率是否为定值,请说明理由.
的斜率是否为定值,请说明理由.
已知函数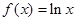 ,
,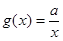 ,
,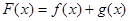 .
.
(1)当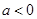 时,求函数
时,求函数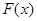 的单调区间;
的单调区间;
(2)若函数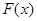 在区间
在区间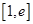 上的最小值是
上的最小值是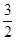 ,求
,求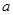 的值;
的值;
(3)设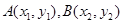 是函数
是函数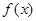 图象上任意不同的两点,线段
图象上任意不同的两点,线段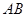 的中点为
的中点为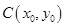 ,直线
,直线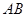 的斜率为
的斜率为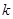 ,证明:
,证明: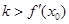 .
.