函数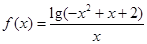 的定义域为( )
的定义域为( )
A.(-1,0) (0,2) (0,2) |
B.(-1,0) (0,+∞) (0,+∞) |
C.(一∞,-1) (2,+∞) (2,+∞) |
D.(-1,2) |
已知集合 ,对任意
,对任意 ,则下列说法错误的是( )
,则下列说法错误的是( )
A. |
B. |
C. |
D. |
已知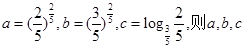 的大小关系是( )
的大小关系是( )
| A.a<c<b | B.b<a<e | C.c<a<b | D.a<b<c |
下列函数中,随x(x>0)的增大,增长速度最快的是( )
| A.y =1,x∈Z | B.y=x | C.y=  |
D.y=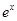 |
 等于( )
等于( )
| A.e2 -2 | B.e一1 | C.e2 | D.e+1 |
原命题为“三角形ABC中,若cosA <0,则三角形ABC为钝角三角形”,关于其逆命题,否命题,逆否命题真假性的判断依次如下,正确的是( )
| A.真,真,真 | B.假,假,真 |
| C.真,真,假 | D.真,假,假 |
已知函数 在区间(0,2)上不是单调函数,则b的取值范围是( )
在区间(0,2)上不是单调函数,则b的取值范围是( )
| A.(一∞,0) | B.(一∞,-2) | C.(-2,0) | D.(-2,+∞) |
函数 的图象大致是( )
的图象大致是( )

下列函数中,与函数 的奇偶性、单调性均相同的是( )
的奇偶性、单调性均相同的是( )
A. |
B.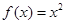 |
C. |
D. |
已知函数 满足
满足 ,在区间[a,2b]上的最大值为e-1,则b为( )
,在区间[a,2b]上的最大值为e-1,则b为( )
| A.ln3 | B.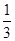 |
C. |
D.l |
已知定义在R上的函数 满足:
满足:
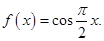 记函数g(x)= f(x)-log4(x+l),则函数g(x)在区间[0,10]内零点个数是( )
记函数g(x)= f(x)-log4(x+l),则函数g(x)在区间[0,10]内零点个数是( )
| A.12 | B.11 | C.10 | D.9 |
函数 在R上可导,下列说法正确的是( )
在R上可导,下列说法正确的是( )
A.若 对任意x 对任意x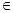 R恒成立,则有 R恒成立,则有 |
B.若 对任意x 对任意x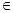 R恒成立,则有 R恒成立,则有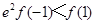 |
C.若 对任意x 对任意x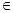 R恒成立,则有 R恒成立,则有 |
D.若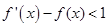 对任意x 对任意x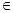 R恒成立,则有 R恒成立,则有 |
命题“任意x∈(0,+∞),都有x2 -2x >0”的否定是____。
如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),f’(x)为 的导函数,则f’(1)+f ‘(4)= 。
的导函数,则f’(1)+f ‘(4)= 。

已知函数 = (2x -a +l)ln(x +a +1)的定义域为(-a -1,+∞),若
= (2x -a +l)ln(x +a +1)的定义域为(-a -1,+∞),若 ≥0恒成立,则a的值是 .
≥0恒成立,则a的值是 .
定义在R的函数y= ,如果函数图象上任意一点都在曲线y2=|x|上,则下列结论正确的是__ (填上所有正确结论的序号)
,如果函数图象上任意一点都在曲线y2=|x|上,则下列结论正确的是__ (填上所有正确结论的序号)
①f(0)=0;
②函数y= 值域为R;
值域为R;
③函数y= 可能既不是奇函数也不是偶函数;
可能既不是奇函数也不是偶函数;
④函数y= 可能不是单调函数;
可能不是单调函数;
⑤函数y= 的图象与直线y=
的图象与直线y= 有三个交点,
有三个交点,
(本小题满分10分)
化简(I)
(Ⅱ)若正实数a,b满是log8a +log2b =5,log8b +1og2a =7,求log2 ab.
(本小题满分12分)
设命题p:实数x满足x2 -2x+l –m2≤0,其中m>0,命题q: ≥1
≥1
(I)若m=2且p q为真命题,求实数x的取值范围;
q为真命题,求实数x的取值范围;
(Ⅱ)若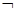 q是
q是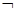 P的充分不必要条件,求实数m的取值范围.
P的充分不必要条件,求实数m的取值范围.
(本小题满分12分)
已知函数 是定义在(一1,1)上的奇函数,且
是定义在(一1,1)上的奇函数,且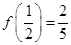
(I)求函数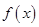 的解析式;
的解析式;
(Ⅱ)证明:函数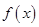 在(-1,1)上是增函数;
在(-1,1)上是增函数;
(Ⅲ)解关于}的不等式,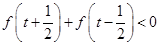 .
.
(本小题满分l2分)
对于定义在区间D上的函数 ,若存在闭区间[a,b]
,若存在闭区间[a,b]  D和常数c,使得对任意x1
D和常数c,使得对任意x1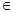 [a,b],都有
[a,b],都有 ,且对任意x2
,且对任意x2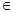 D,当x2
D,当x2 [a,b]时
[a,b]时 恒成立,则称函数f(x)为区间D上的“平底型”函数
恒成立,则称函数f(x)为区间D上的“平底型”函数
(I)若函数 ="|mx-1|" +|x -2|是R上的“平底型”函数,求m的值;
="|mx-1|" +|x -2|是R上的“平底型”函数,求m的值;
(Ⅱ)判断函数 =x+|x-l|是否为R上的“平底型”函数?并说明理由;
=x+|x-l|是否为R上的“平底型”函数?并说明理由;
(Ⅲ)若函数g(x)="px+" |x –q|是区间[0,+∞)上的“平底型”函数,且函数的最小值为1,求p,q
的值.
(本小题满分12分)
已知函数
(I)求函数 的单调区间;
的单调区间;
(Ⅱ)若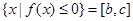 (其中b<c),求a的取值范围,并说明[b,c]
(其中b<c),求a的取值范围,并说明[b,c] (0,1)。
(0,1)。
(本小题满分12分)
已知函数 = 21nx—x2+ax(a
= 21nx—x2+ax(a R)
R)
(I)当a=2时,求 的图象在x=l处的切线方程;
的图象在x=l处的切线方程;
(Ⅱ)若函数 的图象与x轴有两个不同的交点A(x1,0),B( x2,0)(0< x1< x2),
的图象与x轴有两个不同的交点A(x1,0),B( x2,0)(0< x1< x2),
求证: (其中
(其中 为
为 的导函数)
的导函数)