已知集合
，集合
，则集合
（ ）
A．0 B．
C．
D．
命题“若α＝
，则tanα＝1”的逆否命题是（ ）
| A．若α≠，则tanα≠1 |
| B．若α＝，则tanα≠1 |
| C．若tanα≠1，则α＝ |
| D．若tanα≠1，则α≠ |
下列函数中，既是偶函数又在（0，＋∞）上单调递增的是（ ）
A． |
B． |
C． |
D． |
若
对于任意实数
恒有
，则
（ ）
| A．2 | B．0 | C．1 | D．-1 |
已知条件p：
|
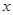+1|＞2，条件q：5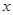﹣6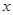＞2，则￢q是￢p的（ ）
| A．充分不必要条件 |
| B．必要不充分条件 |
| C．充要条件 |
| D．既不充分也不必要条件 |
已知
则（ ）
| A．a＞b＞c | B．a＞c＞b | C．c＞b＞a | D．b＞a＞c |
函数
的图象是（ ）
函数
是偶函数且满足
，当
时，
，则不等式
在
上的解集为（ ）
| A．（1，3） | B．（-1，1） | C．（-1，0）∪（1，3） | D．（-2，-1）∪（0，1） |
方程
的解所在的区间是（ ）
A． |
B． |
C． |
D． |
用
表示a,b,c 中的最小值，设
则
的最大值是（ ）
| A．4 | B．6 | C．3 | D．5 |
若[
]表示不超过的最大整数，例如[2．9]＝2，[－4．1]＝－5，已知
（
），
，则函数
的零点个数是（ ）
| A．2016 | B．2015 | C．2014 | D．2013 |
已知
是在R上的可导函数，且
都有
则（ ）
A． |
B． |
C． |
D． |
过定点____．
已知函数
，则
．
已知函数
在（0,1）上是增函数，则实数a的最大值是 ．
设函数
若a,b,c互不相等，且f（a）=f（b）=f（c），则a+b+c的取值范围为 ．
命题p：关于
的不等式
的解集为
，命题q：函数
为增函数．若
为真，
为假,求
的取值范围．
已知二次函数
满足
且
（1）求二次函数的解析式．
（2）求函数
的单调增区间和值域 ．
已知函数
（1）若
,求
在点
处的切线方程；
（2）若
，求函数
在
上的最大值和最小值．
设函数
，
（1）若
，求
取值范围；
（2）求
的最值，并给出最值时对应的
的值．
已知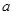
为实数，函数
．
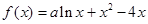（1）是否存在实数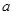，使得
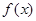在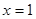
处取得极值？证明你的结论；
（2）设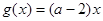
，若
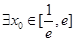，使得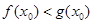
成立，求实数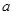的取值范围．
在直角坐标平面内，直线l过点P（1，1），且倾斜角α＝
．以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系，已知圆C的极坐标方程为ρ＝4sinθ．
（1）求圆C的直角坐标方程；
（2）设直线l与圆C交于A、B两点，求|PA|·|PB|的值．
已知
．
（1）解不等式
；
（2）若关于
的不等式
对任意的
恒成立，求
的取值范围．