 =( )
=( )
A.2 |
B.2 | C.1 | D. |
设 145°,
145°, 52°,
52°, 47°,则
47°,则 的大小关系是
的大小关系是
A. |
B. |
C. |
D. |
函数 的零点所在的区间是(
的零点所在的区间是( )( )
)( )
A. |
B. |
C. |
D. |
下列命题中的假命题是( )
A. |
B. |
C. |
D. |
已知集合A= ,B={x|
,B={x| ≤2,x∈Z},则满足条件A
≤2,x∈Z},则满足条件A C
C B的集合C的个数为( )
B的集合C的个数为( )
| A.1 | B.2 | C.4 | D.8 |
设等比数列 的公比
的公比 ,前n项和为
,前n项和为 ,则
,则 ( )
( )
| A.2 | B.4 | C. |
D. |
已知平面向量 =(1,-3),
=(1,-3), =(4,-2),
=(4,-2), 与
与 垂直,则
垂直,则 是( )
是( )
| A.-1 | B.1 | C.-2 | D.2 |
已知cos -sinα=
-sinα= ,则sin
,则sin 的值是( )
的值是( )
A.- |
B.- |
C. |
D. |
设数列 是以3为首项,1为公差的等差数列,
是以3为首项,1为公差的等差数列, 是以1为首项,2为公比的等比数列,则
是以1为首项,2为公比的等比数列,则 =
=
| A.15 | B.72 | C.63 | D.60 |
设函数 的最小值为-1,则实数
的最小值为-1,则实数 的取值范围是
的取值范围是
A. |
B. |
C. |
D. |
已知 中,内角
中,内角 ,
, ,
, 所对的边长分别为
所对的边长分别为 ,
, ,
, .若
.若 ,
, ,
, ,则
,则 的面积等于 ( )
的面积等于 ( )
A. |
B. |
C. |
D. |
对于函数 ,若存在区间
,若存在区间 ,使得
,使得 ,则称函数
,则称函数 为“可等域函数”,区间
为“可等域函数”,区间 为函数
为函数 的一个“可等域区间”.给出下列4个函数:
的一个“可等域区间”.给出下列4个函数:
① ,
,
② ,
,
③ ,
,
④ .
.
其中存在唯一“可等域区间”的“可等域函数”为
| A.①②③ | B.②③ | C.①③ | D.②③④ |
已知向量a,b,满足|a|=1,| b |= ,a+b=(
,a+b=( ,1),则向量a与b的夹角是 .
,1),则向量a与b的夹角是 .
若等比数列{an}的各项均为正数,且a10a11+a9a12=2e5,则 .
在△ABC中,若tanB=-2,cosC= ,则角A= .
,则角A= .
已知函数f(x)=x2+ ,g(x)=
,g(x)= -m.若
-m.若 x1∈[1,2],
x1∈[1,2], x2∈[-1,1]使f(x1)≥g(x2),则实数m的取值范围是 .
x2∈[-1,1]使f(x1)≥g(x2),则实数m的取值范围是 .
(本小题满分10分)设 是等差数列,
是等差数列, 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且 ,
, ,
, .
.
(1)求 ,
, 的通项公式;
的通项公式;
(2)求数列 ,
, 的前
的前 项和
项和 和
和
(本小题满分12分)已知函数 .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)求函数 的最大值及最小值;
的最大值及最小值;
(3)写出 的单调递增区间.
的单调递增区间.
(本小题满分12分)已知函数f(x)=log3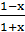 .
.
(1)求函数f(x)的定义域.
(2)判断函数f(x)的奇偶性.
(3)当x∈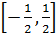 时,函数g(x)=f(x),求函数g(x)的值域.
时,函数g(x)=f(x),求函数g(x)的值域.
(本小题满分12分)设数列{an}的前n项和为Sn=n2,{bn}为等比数列,且a1=b1,b2(a2-a1)=b1.
(1)求数列{an},{bn}的通项公式.
(2)设cn=an·bn,求数列{cn}的前n项和Tn.
(本小题满分12分)设△ABC三个内角A、B、C所对的边分别为a,b,c.已知C= ,acosA=bcosB.
,acosA=bcosB.
(1)求角B的大小;
(2)如图,在△ABC内取一点P,使得PB=2.过点P分别作直线BA、BC的垂线PM、PN,垂足分别是M、N.设∠PBA= ,求PM+PN的最大值及此时
,求PM+PN的最大值及此时 的取值.
的取值.
(本小题满分12分).已知函数 (
( ).
).
(1)若 ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)若不等式 对任意
对任意 恒成立.
恒成立.
(ⅰ)求实数 的取值范围;
的取值范围;
(ⅱ)试比较 与
与 的大小,并给出证明(
的大小,并给出证明( 为自然对数的底数,
为自然对数的底数, ).
).