已知集合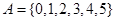 ,
,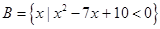 ,则
,则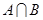 的子集可以是
的子集可以是
A.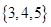 |
B.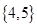 |
C.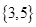 |
D.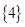 |
若复数 是虚数单位)是纯虚数,则复数
是虚数单位)是纯虚数,则复数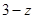 的共轭复数是
的共轭复数是
A.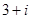 |
B.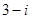 |
C.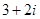 |
D.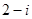 |
已知抛物线 ,则
,则
A.它的焦点坐标为 |
B.它的焦点坐标为 |
C.它的准线方程是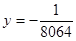 |
D.它的准线方程是 |
下列说法中,不正确的是
A.“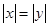 ”是“ ”是“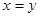 ” 的必要不充分条件 ” 的必要不充分条件 |
B.命题“若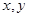 都是奇数,则 都是奇数,则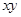 是奇数”的否命题是“若 是奇数”的否命题是“若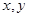 不都是奇数,则 不都是奇数,则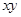 不是奇数” 不是奇数” |
C.命题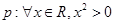 或 或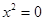 ,则 ,则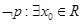 使 使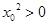 或 或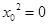 |
D.命题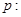 若回归方程为 若回归方程为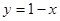 ,则 ,则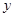 与 与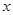 正相关;命题 正相关;命题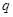 :若 :若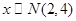 ,则 ,则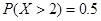 ,则 ,则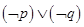 为真命题 为真命题 |
已知倾斜角为 的直线
的直线 与直线
与直线 垂直,则
垂直,则 的值为
的值为
A. |
B. |
C. |
D. |
给出以下数阵,按各数排列规律,则 的值为
的值为
A. |
B. |
C. |
D.326 |
运行如下程序框图:
若输出的的 值为12,则判断框中
值为12,则判断框中 的值可以是
的值可以是
| A.2 | B.3 | C.4 | D.5 |
已知向量 ,则函数
,则函数 的最小正周期与最大值分别为
的最小正周期与最大值分别为
A. |
B. |
C. |
D. |
已知一个几何体的三图如图所示,山该几何体的体积为
A. |
B. |
C. |
D. |
2015年4月22日,亚非领导人会议在印尼雅加达举行,某五国领导人
 、
、 、
、 、
、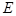 除
除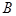 与
与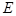 、
、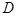 与
与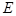 不单独会晤外,其他领导人两两之间都要单独会晤.现安排他们在两天的上午、下午单独会晤(每人每个半天最多进行一次会晤),那么安排他们单独会晤的不同方法共有
不单独会晤外,其他领导人两两之间都要单独会晤.现安排他们在两天的上午、下午单独会晤(每人每个半天最多进行一次会晤),那么安排他们单独会晤的不同方法共有
| A.48种 | B.36种 | C.24种 | D.8种 |
设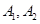 分别为双曲线
分别为双曲线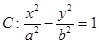
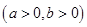 的左右顶点,若双曲线上存在点
的左右顶点,若双曲线上存在点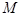 使得两直线斜率
使得两直线斜率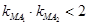 ,则双曲线
,则双曲线 的离心率的取值范围为
的离心率的取值范围为
A.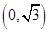 |
B.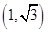 |
C.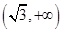 |
D.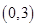 |
已知定义域为 的函数
的函数 ,若对任意的
,若对任意的 ,有
,有 ,则称函数
,则称函数 为“定义域上的
为“定义域上的 函数”,以下五个函数:①
函数”,以下五个函数:① ;②
;② ; ③
; ③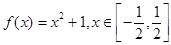 ;④
;④ ;⑤
;⑤ ,其中是“定义上的
,其中是“定义上的 函数”的有
函数”的有
| A.2个 | B.3个 | C.4个 | D.5个 |
已知 展开式的常数项为15,则展开式的各项系数和为 .
展开式的常数项为15,则展开式的各项系数和为 .
已知 满足
满足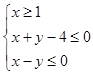 ,,记
,,记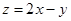 的最大值为
的最大值为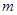 ,则函数
,则函数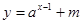 (
(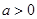 且
且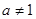 )的图象所过定点坐标为 .
)的图象所过定点坐标为 .
已知数列 是等比数列,且
是等比数列,且 ,则
,则
.
在锐角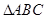 中,内角
中,内角 、
、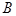 、
、 的对边分别为
的对边分别为 、
、 、
、 ,已知
,已知 ,
, ,则
,则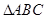 的面积取最大值时有
的面积取最大值时有 .
.
(本小题满分12分)
设数列 满足
满足 ,且对任意
,且对任意 ,函数
,函数 满足
满足 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,记数列
,记数列 的前项和为
的前项和为 ,求证:
,求证: .
.
(本小题满分12分)
微信是腾讯公司推出的一种手机通讯软件,它支持发送语音短信、视频、图片和文字,一经推出便风靡全国,甚至涌现出一批在微信的朋友圈内销售商品的人(被称为微商).为了调查每天微信用户使用微信的时间,某经销化妆品的微商在一广场随机采访男性、女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
| |
微信控 |
非微信控 |
合计 |
| 男性 |
26 |
24 |
50 |
| 女性 |
30 |
20 |
50 |
| 合计 |
56 |
44 |
100 |
(1)根据以上数据,能否有 ﹪的把握认为“微信控”与“性别”有关?
﹪的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人赠送营养面膜1份,求所抽取5人中“微信控”和“非微信控”的人数;
(3)从(2)中抽取的5人中再随机抽取3人赠送200元的护肤品套装,记这3人中“微信控”的人数为 ,试求
,试求 的分布列与数学期望.
的分布列与数学期望.
参考公式: ,其中
,其中 .
.
参考数据:
 |
0.50 |
0.40 |
0.25 |
0.05 |
0.025 |
0.010 |
 |
0.455 |
0.708 |
1.321 |
3.840 |
5.024 |
6.635 |
(本小题满分12分)
如图,已知四棱锥 中,
中, 平面
平面 ,底面
,底面 是正方形,
是正方形, 、
、 分别为
分别为 、
、 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求二面角 的余弦值.
的余弦值.
(本小题满分12分)
已知椭圆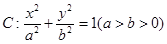 的离心率为
的离心率为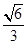 ,以原点
,以原点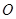 为圆心,椭圆
为圆心,椭圆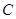 的长半轴这半径的圆与直线
的长半轴这半径的圆与直线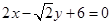 相切.
相切.
(1)求椭圆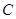 标准方程;
标准方程;
(2)已知点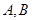 为动直线
为动直线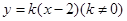 与椭圆
与椭圆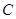 的两个交点,问:在
的两个交点,问:在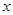 轴上是否存在点
轴上是否存在点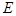 ,使
,使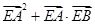 为定值?若存在,试求出点
为定值?若存在,试求出点 的坐标和定值,若不存在,说明理由.
的坐标和定值,若不存在,说明理由.
(本小题满分12分)
已知函数 ,且曲线
,且曲线 在点
在点 处的切线与直线
处的切线与直线 平行.
平行.
(1)求 的值;
的值;
(2)判断函数 的单调性;
的单调性;
(3)求证:当 时,
时,
(本小题满分10分)
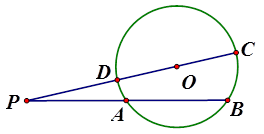
自圆 外一点
外一点 引圆
引圆 的两条割线
的两条割线 和
和 ,如图所示,其中割线
,如图所示,其中割线 过圆心
过圆心 ,
, .
.
(1)求 的大小;
的大小;
(2)分别求线段 和
和 的长度.
的长度.
(本小题满分10分)
已知在直角坐标系 中,圆
中,圆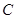 的参数方程为
的参数方程为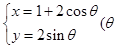 为参数).
为参数).
(1)以原点为极点、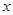 轴正半轴为极轴建立极坐标系,求圆
轴正半轴为极轴建立极坐标系,求圆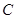 的极坐标方程;
的极坐标方程;
(2)直线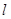 的坐标方程是
的坐标方程是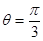 ,且直线
,且直线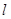 与圆
与圆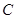 交于
交于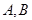 两点,试求弦
两点,试求弦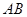 的长.
的长.
(本小题满分10分)
已知函数 的定义域为
的定义域为 .
.
(1)求实数 的取值范围;
的取值范围;
(2)当正数 满足
满足 时,求
时,求 的最小值.
的最小值.