的绝对值是（ ）
| A．－3 | B． |
C．3 | D． |
南海初级中学的校园面积约是102000平方米，用科学记数法表示为（ ）
| A．1．02×105 | B．10．2×104 | C．102×103 | D．0．102×106 |
下列说法不正确 的是（ ）
| A．0既不是正数，也不是负数 |
| B．1是绝对值最小的正数 |
| C．一个有理数不是整数就是分数 |
| D．0的绝对值是0 |
下列各式正确的是（ ）
A． |
B．+（-3）＝3 | C． |
D．－（-3）＝-3 |
某月的月历，竖着取连续的三个数字，它们的和可能是（ ）
| A．18 | B．33 | C．38 | D．75 |
若
，则
=（ ）
| A．－9 | B．9 | C．27 | D．－27 |
若规定“!”是一种数学运算符号，且
则
的值为（ ）
A． |
B．99! | C．9 900 | D．2! |
古希腊著名的毕达哥拉斯学派把1、3、6、10 … 这样的数称为“三角形数”，而把1、4、9、16 … 这样的数称为“正方形数”．从图中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和．下列等式中，符合这一规律的是（ ）
| A．36=15+21 | B．49=18+31 | C．25="9+16" | D．13=3+10 |
如果把向西走2米记为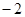
米，则向东走3米表示为 米；
绝对值小于4的所有整数的和是 ．
（－5）－（ ）＝1
按你发现的规律填数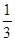
、—
、
、—
、 _、…
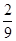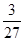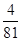定义一种新运算：
※
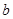
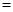
，如
※
=
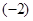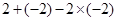=4，那么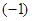
※
= ．
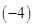高邮某天上午的温度是25℃，中午又上升了3℃，下午由于冷空气南下，到夜间又下降到15
℃，则这天的温差是 ℃。
比较大小：
．
已知︱-x︱=︱-8︱，x= ．
计算：（1-2）
（2-3）（3-4）………（2013-2014）= ．
有一个正六面体骰子，放在桌面上，将骰子沿如图所示的顺时针方向滚动，每滚动
算一次，则滚动第2015次后，骰子朝下一面的点数是 ．
（本题8分）将下列各数填入相应的集合中．
—7，0，
，—22
，-2．55555…，3．01，+9 ，-2
．+10﹪，
4．020020002…（每两个2之间依次增加
个0），
无理数集合：{ … }；
负有理数集合：{ …}；
正分数集合：{ … }；
非负整数集合：{ …}；
（本题8分）把下列各数在数轴上表示，并从小到大的顺序用“＜”连接起来。
计算．（每题4分，共24分）
（1）
（2）
（3）
（4）（-81）
（5）
（6）
（本题8分）定义新运算。
，如
，计算下列各式。
（1）
（2）
（本题8分）已知在纸面上有一数轴（如图），折叠纸面．
（1）若1表示的点与－1表示的点重合，则－2表示的点与数 表示的点重合；
（2）若－1表示的点与3表示的点重合，回答以下问题：
①5表示的点与数 表示的点重合；
②若数轴上A、B两点之间的距离为6（A在B的左侧），且A、B两点经折叠后重合，则A点表示数是
（本题6分）如图是计算机程序计算图。
（1）若开始输入为－1，请你根据程序列出综合算式并计算出输出结果；
（2）若最后输出为－1，请你求输入的值。（不要求写出过程）
（本题8分）小明有5张写着不同数字的卡片，请你按要求抽出卡片，完成下列各问题：
（1）从中取出2张卡片，使这2张卡片上数字的乘积最小，乘积的最小值为 ；
（2）从中取出4张卡片，用学过的运算方法，使结果为24。写出运算式子。
（写出一种即可）算24的式子为 。
（本题8分）已知：
，
，且
，求
的值．
（本题9分）数轴上的点M对应的数是-4，一只甲虫从M点出发沿数轴以每秒2个单位长度的速度爬行，当它到达数轴上的N点后，立即返回到原点，共用11秒．
（1）甲虫爬行的路程是多少？
（2）点N对应的数是多少？
（3）点M和点N之间的距离是多少？
（本题9分）我们都知道无限不循环小数是无理数，而无限循环小数是可以化成分数的。例如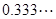
（3为循环节）是可以化成分数的，方法如下：
令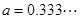
①
则
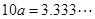②
②-①得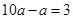
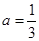
所以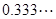可以化成分数为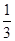
请你阅读上面材料完成下列问题：
（1）
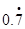化成分数是 ．
（2）请你将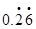 
化为分数．
（3）请你将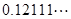
（即
）化为分数．