设 ,则
,则 是
是 的 ( )
的 ( )
| A.充分不必要条件 |
| B.必要不充分条件 |
| C.充要条件 |
| D.既不充分也不必要条件 |
给定下列四个命题:
①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;
②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;
③垂直于同一直线的两条直线相互平行;
④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.
其中,为真命题的是 ( )
| A.①和② | B.②和③ | C.③和④ | D.②和④ |
已知函数 的最小正周期为
的最小正周期为 ,为了得到函数
,为了得到函数 的图象,只要将
的图象,只要将 的图象 ( )
的图象 ( )
A.向左平移 个单位长度 个单位长度 |
B.向右平移 个单位长度 个单位长度 |
C.向左平移 个单位长度 个单位长度 |
D.向右平移 个单位长度 个单位长度 |
已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的体积是 ( )

| A.2 | B.4 | C.6 | D. |
已知 为第二象限角,
为第二象限角, ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
称 为两个向量
为两个向量 间的“距离”,若向量
间的“距离”,若向量 满足:
满足:
(1) ;(2)
;(2) ;(3)对任意的
;(3)对任意的 ,恒有
,恒有 ,则 ( )
,则 ( )
A. |
B. |
C. |
D. |
已知直线 与抛物线C:
与抛物线C: 相交A、B两点,F为C的焦点.若
相交A、B两点,F为C的焦点.若 ,则k= ( )
,则k= ( )
A. B.
B. C.
C. D.
D.
已知函数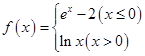 ,则下列关于函数
,则下列关于函数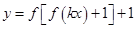 (
( )的零点个数的判断正确的是 ( )
)的零点个数的判断正确的是 ( )
A.当 时,有 时,有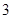 个零点;当 个零点;当 时,有 时,有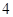 个零点 个零点 |
B.当 时,有 时,有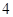 个零点;当 个零点;当 时,有 时,有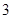 个零点 个零点 |
C.无论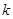 为何值,均有 为何值,均有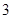 个零点 个零点 |
D.无论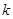 为何值,均有 为何值,均有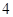 个零点 个零点 |
双曲线 的焦点坐标是 ,渐近线方程是 .
的焦点坐标是 ,渐近线方程是 .
设集合 ,
, ,若
,若 ,则
,则 的取值范围为 ; 若
的取值范围为 ; 若 ,则
,则 的取值范围为 .
的取值范围为 .
若x, y满足约束条件 则点P(x, y)构成的区域的面积为 ;
则点P(x, y)构成的区域的面积为 ; 的最大值为 .
的最大值为 .
已知数列 满足:
满足: 则
则 = ;
= ; = .
= .
如图,四边形ABCD和ADPQ均为正方形,它们所在的平面互相垂直,M,E,F分别为PQ,AB,BC的中点,则异面直线EM与AF所成的角的余弦值是 .

已知正数x,y满足:x+4y=xy,则x+y的最小值为 .
函数 ,
, ,
, ,
, ,对任意的
,对任意的 ,总存在
,总存在 ,使得
,使得 成立,则
成立,则 的取值范围为 .
的取值范围为 .
在△ABC中,a、b、c分别是角A、B、C的对边,且 .
.
(Ⅰ)求角B的大小;
(Ⅱ)若 ,求△ABC的面积.
,求△ABC的面积.
如图,在直三棱柱 中,
中, 平面
平面 ,其垂足
,其垂足 落在直线
落在直线 上.
上.
(Ⅰ)求证: ⊥
⊥ ;
;
(Ⅱ)若 ,
, ,
, 为
为 的中点,求二面角
的中点,求二面角 的平面角的余弦值.
的平面角的余弦值.
(本小题满分14分)已知函数 .
.
(Ⅰ)若当 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(Ⅱ)求函数 在区间
在区间 上的最大值.
上的最大值.
已知数列 满足
满足 ,且
,且 ,
, 为
为 的前
的前 项和.
项和.
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)如果对于任意 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.