已知集合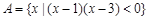 ,
,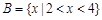 ,则
,则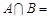
A.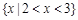  |
B.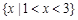 |
C.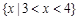 |
D.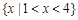 |
已知等差数列 中,若
中,若 则公差
则公差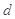 =
=
A.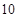 |
B. |
C.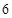 |
D.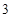 |
设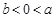 ,
,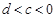 ,则下列各不等式中恒成立的是
,则下列各不等式中恒成立的是
A.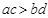 |
B.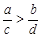 |
C.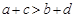 |
D.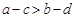 |
与直线 关于
关于 轴对称的直线方程是
轴对称的直线方程是
A. |
B. |
C. |
D. |
圆 被直线
被直线 截得的弦长是
截得的弦长是
A. |
B. |
C. |
D. |
如图,在山顶 测得山下塔顶
测得山下塔顶 和塔底
和塔底 的俯角分别为30°和60°,已知塔高
的俯角分别为30°和60°,已知塔高 为
为 ,则山高
,则山高 为
为
A. |
B. |
C. |
D. |
已知实数 ,
, 满足
满足 ,则
,则 的最小值是
的最小值是
| A.1 | B.2 |
| C.4 | D.10 |
关于实数 的不等式
的不等式 的解集是
的解集是 ,则关于
,则关于 的不等式
的不等式 的解集是
的解集是
A. |
B. |
C. |
D. |
若直线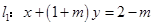 与
与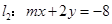 平行,则实数
平行,则实数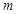 的值为
的值为
A. 或 或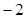 |
B. |
C.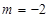 |
D.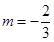 |
若定义域为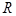 的奇函数
的奇函数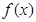 满足
满足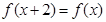 ,且在
,且在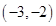 上单调递减,则
上单调递减,则
A.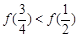 |
B.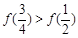 |
C.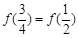 |
D.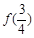 与 与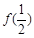 的大小不确定 的大小不确定 |
若直线 (其中
(其中 且
且 )平分圆
)平分圆 的周长,则
的周长,则 的最小值为
的最小值为
A. |
B. |
C. |
D. |
已知矩形 , 点
, 点 满足
满足 ,
, ,则
,则 的最大值是
的最大值是
A. |
B. |
C. |
D. |
过点 ,且倾斜角为45°的直线的方程是 .
,且倾斜角为45°的直线的方程是 .
在等差数列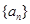 中,若
中,若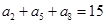 ,则数列
,则数列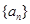 的前9项和
的前9项和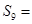 .
.
已知点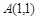 ,
, ,若直线
,若直线 :
: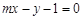 与线段
与线段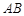 相交,则实数
相交,则实数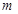 的取值范围为 .
的取值范围为 .
已知函数 其中
其中 为自然对数的底数,若关于
为自然对数的底数,若关于 的方程
的方程 有且只有一个实数根,则实数
有且只有一个实数根,则实数 的取值范围是 .
的取值范围是 .
(本小题满分10分)(注意:在试题卷上作答无效)
在锐角 中,角
中,角 、
、 、
、 的对边分别为
的对边分别为 ,且
,且 .
. 求角
求角 的大小;
的大小; 若
若 ,求
,求 的面积.
的面积.
(本小题满分12分)(注意:在试题卷上作答无效)
已知函数 .
. 求
求 的最小正周期;
的最小正周期; 求
求 在
在 上的最值.
上的最值.
(本小题满分12分)(注意:在试题卷上作答无效)
在平面直角坐标系 中,已知
中,已知 ,
, .
. 若
若 ∥
∥ ,求
,求 的坐标;
的坐标; 若
若 与
与 垂直,求
垂直,求 与
与 的夹角
的夹角 的大小.
的大小.
(本小题满分12分)(注意:在试题卷上作答无效)
在平面直角坐标系 中,已知直线
中,已知直线 与圆心在第二象限的圆
与圆心在第二象限的圆 相切于原点
相切于原点 ,且圆
,且圆 与圆
与圆
 的面积相等.
的面积相等. 求圆
求圆 的标准方程;
的标准方程; 试探究圆
试探究圆 上是否存在异于原点的点
上是否存在异于原点的点 ,使点
,使点 到定点
到定点 的距离等于线段
的距离等于线段 的长?若存在,求出点
的长?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(本小题满分12分)(注意:在试题卷上作答无效)
已知定义在 上的函数
上的函数 ,对任意
,对任意 都有
都有 ,且
,且 是
是 上的增函数.
上的增函数.
 求证:函数
求证:函数 是
是 上的奇函数;
上的奇函数;
 若不等式
若不等式 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分12分)(注意:在试题卷上作答无效)
已知数列 的前
的前 项和
项和 满足
满足 ,数列
,数列 满足
满足 ,其中
,其中 .
. 求数列
求数列 和
和 的通项公式;
的通项公式; 设
设 ,数列
,数列 的前
的前 项和为
项和为 ,若
,若 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.