下列方程是一元二次方程的是( )
A.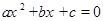 |
B.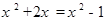 |
C.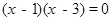 |
D.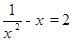 |
一元二次方程 化成一般形式
化成一般形式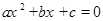 后,若a="2" ,则b,c的值是( )
后,若a="2" ,则b,c的值是( )
| A.b=3,c=5 | B.b= ,c=5 ,c=5 |
C.b= ,c= ,c=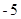 |
D.b=3,c=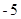 |
抛物线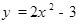 的顶点在( )
的顶点在( )
| A.第一象限 | B.第二象限 | C.x轴上 | D.y轴上 |
用配方法解一元二次方程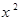 +8x+7=0,则方程可变形为( )
+8x+7=0,则方程可变形为( )
A.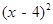 =9 =9 |
B.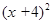 =9 =9 |
C.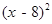 =16 =16 |
D.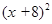 ="57" ="57" |
二次函数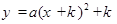 ,当k取不同的实数值时,图像顶点所在的直线是( )
,当k取不同的实数值时,图像顶点所在的直线是( )
A. |
B.x轴 | C.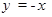 |
D.y轴 |
下列方程中两根互为倒数有( )



| A.0个 | B. 1个 | C. 2个 | D.3个 |
把抛物线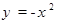 向右平移一个单位,再向上平移3个单位,得到抛物线的解析式为( )
向右平移一个单位,再向上平移3个单位,得到抛物线的解析式为( )
A.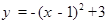 |
B.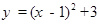 |
C.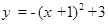 |
D.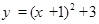 |
为解决群众看病贵的问题,有关部门决定降低药价,对某种原价为289元的药品进行连续两次降价后为256元,设平均每次降价的百分率为 ,则下面所列方程正确的是( )
,则下面所列方程正确的是( )
A. |
B. |
C. |
D. |
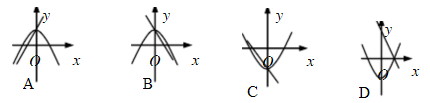
在同一直角坐标系中,一次函数 和二次函数
和二次函数 的图像是( )
的图像是( )
已知a,b为实数,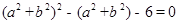 ,则
,则 代数式
代数式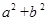 的值为( )
的值为( )
| A.2 | B.3 | C.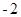 |
D.3或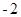 |
若代数式(x+3)(3x-2)的值为4,则x的值是 。
已知方程 的一根是1,.则另一根为__________,k的值为____________。
的一根是1,.则另一根为__________,k的值为____________。
抛物线 的开口向 ,对称轴是直线_____________,顶点坐标为_____。
的开口向 ,对称轴是直线_____________,顶点坐标为_____。
关于x的方程 kx2-2x+1=0有两个不相等的实数根,则k的取值范围是 。
在长宽高为10cm、8cm的矩形纸片中央挖掉一个矩形,得到一个四边等宽的矩形方框,如果挖掉部分的面积为24cm2,则方框的边宽是_________.
已知二次函数 ,若当x取
,若当x取 ,
, (
( ≠
≠ )时,函数值相等,则当x取
)时,函数值相等,则当x取 +
+ 时,函数值为______________.
时,函数值为______________.
解方程
(1)
(2)(x+3)(x-6)=
已知二次函数当x= 时,有最大值
时,有最大值 ,且当x=0时,y=
,且当x=0时,y= ,求二次函数的解析式。
,求二次函数的解析式。
已知直线经过y=kx+b经过(—2,0)(1,6),求不等式kx+b≥ -x的解集。
关于x的一元二次方程(a-6)x2-8x+9=0有实根.
(1)求a的最大整数值;
(2)当a取最大整数值时,
①求出该方程的根;
②求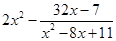 的值.
的值.
关于x的方程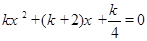 有实数根.
有实数根.
(1)求k的取值范围.
(2)若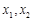 是方程
是方程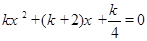 的两个实数根,且满足,kx1-12x1x2=-kx2求k.
的两个实数根,且满足,kx1-12x1x2=-kx2求k.
李师傅去年开了一家商店,今年1月份开始盈利,2月份盈利2400元,4月份盈利3456元,且2到4月,每月盈利平均增长率相同
(1)求每月盈利的平均增长率
(2)按照这个平均增长率,预计5月份这家商店盈利达到多少元?
如图,抛物线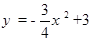 与x轴交于A,B两点,与直线
与x轴交于A,B两点,与直线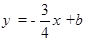 相交于B,C两点,连结A,C两点。
相交于B,C两点,连结A,C两点。 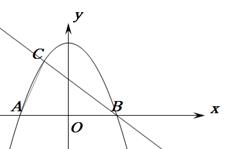
(1)写出直线BC的解析式
(2)求△ABC的面积
如图,利用一面墙(墙的长度为20m),用34m长的篱笆围成两个鸡场,中间用一道篱笆隔开,每个鸡场均留一道1m宽的门,设AB的长为x米。
(1)若两个鸡场总面积为96m2,求x;
(2)若两个鸡场的面积和为S,求S关于x的关系式;
(3)两个鸡场面积和S有最大值吗?若有,最大值是多少?