已知集合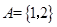 ,
,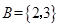 ,则
,则 .
.
函数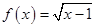 的定义域是
的定义域是
已知幂函数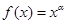 的图象过
的图象过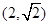 ,则
,则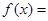 .
.
函数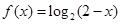 在
在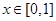 上的最大值为 .
上的最大值为 .
满足不等式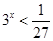 的实数
的实数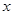 的取值范围是 .
的取值范围是 .
著名的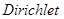 函数
函数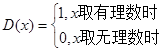 ,则
,则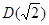 =_________.
=_________.
若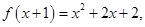 ,则
,则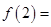 ___________.
___________.
计算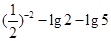 =_______________.
=_______________.
已知函数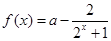 是奇函数,则实数
是奇函数,则实数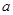 的值为______________.
的值为______________.
若函数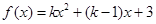 是偶函数,则
是偶函数,则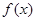 的递减区间是 .
的递减区间是 .
若函数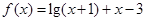 的零点为
的零点为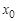 ,满足
,满足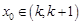 且
且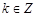 ,则k= .
,则k= .
已知函数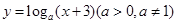 的图象过定点
的图象过定点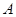 ,若点
,若点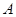 也在函数
也在函数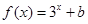 的图象上,则
的图象上,则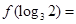 .
.
已知定义在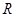 上的函数
上的函数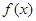 是满足
是满足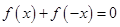 ,在
,在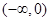 上
上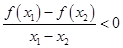 ,且
,且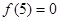 ,则使
,则使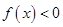 的
的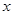 取值范围是___________.
取值范围是___________.
已知函数 ,若
,若 且
且 ,则
,则 的取值范围是 .
的取值范围是 .
已知全集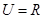 ,集合
,集合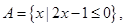
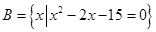 .
.
(1)分别求 、
、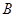 ;
;
(2)求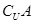 和
和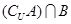 .
.
已知函数f(x)=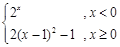 .
.
(1)写出函数f(x)的单调减区间;
(2)求解方程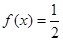 .
.
已知函数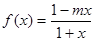 .
.
(1)当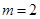 时,用定义证明:
时,用定义证明: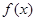 在
在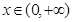 上的单调递减;
上的单调递减;
(2)若不恒为0的函数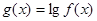 是奇函数,求实数
是奇函数,求实数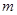 的值.
的值.
姜堰某化学试剂厂以x千克/小时的速度匀速生产某种产品(生产条件要求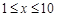 ),每小时可获得的利润是
),每小时可获得的利润是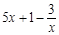 千元.
千元.
(1)要使生产该产品2小时获得利润不低于30千元,求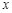 的取值范围;
的取值范围;
(2)要使生产120千克该产品获得的利润最大,问:该工厂应该选取何种生产速度?并求此最大利润.
已知函数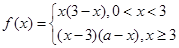 .
.
(1)求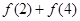 的值;
的值;
(2)若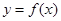 在
在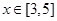 上单调增,在
上单调增,在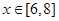 上单调减,求实数
上单调减,求实数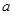 的取值范围;
的取值范围;
(3)设函数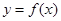 在区间
在区间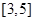 上的最大值为
上的最大值为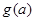 ,试求
,试求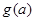 的表达式.
的表达式.
已知函数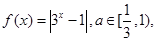 若函数
若函数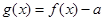 有两个不同的零点
有两个不同的零点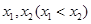 ,函数
,函数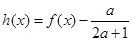 有两个不同的零点
有两个不同的零点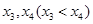 .
.
(1)若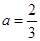 ,求
,求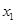 的值;
的值;
(2)求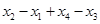 的最小值.
的最小值.