已知 ,
, ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
命题“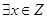 ,使
,使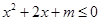 ”的否定是( )
”的否定是( )
A.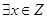 ,使 ,使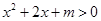 |
B.不存在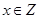 ,使 ,使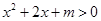 |
C.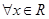 ,使 ,使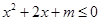 |
D.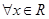 ,使 ,使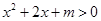 |
在 中,若点
中,若点 满足
满足 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
为了纪念抗日战争胜利 周年,从甲、乙、丙等5名候选民警中选2名作为阅兵安保人员,为9月3号的阅兵提供安保服务,则甲、乙、丙中有2个被选中的概率为( )
周年,从甲、乙、丙等5名候选民警中选2名作为阅兵安保人员,为9月3号的阅兵提供安保服务,则甲、乙、丙中有2个被选中的概率为( )
A. |
B. |
C. |
D. |
函数 与
与 在同一直角坐标系下的图象大致是( )
在同一直角坐标系下的图象大致是( )

设 ,
, ,
, ,
, ,
, ,
, ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
由曲线 ,直线
,直线 ,
, 及
及 轴所围成图形的面积是( )
轴所围成图形的面积是( )
A. |
B. |
C. |
D. [ [ |
已知集合 ,
, ,从
,从 到
到 的映射
的映射 满足
满足 ,那么映射
,那么映射 的个数为( )
的个数为( )
A. |
B. |
C. |
D. |
若函数 ,
, 分别是
分别是 上的奇函数、偶函数,且满足
上的奇函数、偶函数,且满足 ,则( )
,则( )
A. |
B. |
C. |
D. |
《九章算术》“竹九节”问题:现有一根九节的竹子,自上而下各节的容积成等差数列,上面 节的容积共3升,下面3节的容积共4升,则第五节的容积为( )
节的容积共3升,下面3节的容积共4升,则第五节的容积为( )
A. 升 升 |
B. 升 升 |
C. 升 升 |
D.1升 |
下列命题中是假命题的是( )
A. ,使 ,使 是幂函数,且在 是幂函数,且在 上递减 上递减 |
B.函数 的值域为 的值域为 ,则 ,则 或 或 |
C.关于 的方程 的方程 至少有一个负根的充要条件是 至少有一个负根的充要条件是 |
D.函数 与函数 与函数 的图象关于直线 的图象关于直线 对称 对称 |
设 ,已知函数
,已知函数 的定义域是
的定义域是 ,值域是
,值域是 ,若函数
,若函数 有唯一的零点,则
有唯一的零点,则 ( )
( )
| A.2 | B. |
C.1 | D.0 |
已知集合 ,
, ,若
,若 ,则实数
,则实数 的所有可能取值的集合为
的所有可能取值的集合为
若 ,且
,且 ,则
,则

已知点 ,
, ,
, ,
, ,则向量
,则向量 在
在 方向上的投影为
方向上的投影为 .
.
已知函数 ,给出下列四个命题:
,给出下列四个命题:
①存在实数 ,使得函数恰有2个不同的零点;
,使得函数恰有2个不同的零点;
②存在实数 ,使得函数恰有4个不同的零点;
,使得函数恰有4个不同的零点;
③存在实数 ,使得函数恰有5个不同的零点;
,使得函数恰有5个不同的零点;
④存在实数 ,使得函数恰有8个不同的零点.
,使得函数恰有8个不同的零点.
其中真命题的序号是 (把你认为正确的序号全写上).
(把你认为正确的序号全写上).
(本小题满分10分)设命题 函数
函数 的定义域为
的定义域为 ;命题
;命题 不等式
不等式 对一切正实数
对一切正实数 均成立..
均成立..
(1)如果 是真命题,求实数
是真命题,求实数 的取值范围;
的取值范围;
(2)如果命题“ ”为真命题,且“
”为真命题,且“ ”为假命题,求实数
”为假命题,求实数 的取值范围.
的取值范围.
(本小题满分12分)已知二次函数 的图象经过坐标原点,其导函数为
的图象经过坐标原点,其导函数为 .数列
.数列 的前
的前 项和为
项和为 ,点
,点
 均在函数
均在函数 的图象上.
的图象上.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,
, 是数列
是数列 的前
的前 项和,求使得
项和,求使得 对所有
对所有 都成立的最小正整数
都成立的最小正整数 .
.
(本小题满分12分)在 中,角
中,角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, ,已知向量
,已知向量 ,
, ,且
,且 .
.
(1)求角 的大小;
的大小;
(2)若 ,求
,求 面积的最大值.
面积的最大值.
(本小题满分12分)为了解决西部地区某希望小学的师生饮水问题,中原名校联谊会准备援建一个无盖的圆柱形蓄水池(不计厚度),设该蓄水池底面半径为 米,高
米,高 米,体积为
米,体积为 立方米.假设建造成本仅与表面积有关,侧面的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为
立方米.假设建造成本仅与表面积有关,侧面的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为 元(
元( 为圆周率).
为圆周率).
(1)将 表示成
表示成 的函数
的函数 ,并求函数的定义域;
,并求函数的定义域;
(2)讨论函数 的单调性,并确定
的单调性,并确定 和
和 为何值时该蓄水池的体积最大.
为何值时该蓄水池的体积最大.
(本小题满分12分)已知 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,若
,若 ,
, ,
, 时,有
时,有 成立.
成立.
(1)判断 在
在 上的单调性,并证明;
上的单调性,并证明;
(2)解不等式: ;
;
(3)若 对所有的
对所有的 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分12分)已知函数 (
( ).
).
(1)若 为
为 的极值点,求实数
的极值点,求实数 的值;
的值;
(2)若 在
在 上为增函数,求实数
上为增函数,求实数 的取值范围;
的取值范围;
(3)当 时,函数
时,函数 有零点,求实数
有零点,求实数 的最大值.
的最大值.