若集合 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
若幂函数 的图像过点
的图像过点 ,则
,则 的值为( )
的值为( )
| A.6 | B.9 | C.16 | D.27 |
下列函数中,与函数 相同的函数是( )
相同的函数是( )
A. |
B. |
C. |
D. |
三个数 的大小顺序是( )
的大小顺序是( )
A. |
B. |
C. |
D. |
2015年孝感高中学生运动会,某班62名学生中有一半的学生没有参加比赛,参加比赛的同学中,参加田赛的有16人,参加径赛的有23人,则田赛和径赛都参加的学生人数为( )
| A.7 | B.8 | C.10 | D.12 |
已知函数 在区间
在区间 上是单调递增函数,则实数
上是单调递增函数,则实数 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
下列函数中为偶函数的是( )
A. . . |
B. |
C. |
D. |
某学生离家去学校,由于怕迟到,所以一开始就匀速跑步,等跑累了再匀速走余下的路程.在下图中纵轴表示离学校的距离,横轴表示出发后的时间,则下图的四个图形中较符合该学生走法的是( )

使得函数 有零点的一个区间是( )
有零点的一个区间是( )
| A.(0,1) | B.(1,2) | C.(2,3) | D.(3,4) |
已知函数 ,若
,若 ,则
,则 ( )
( )
| A.0 | B.3 | C.4 | D.6 |
设集合 ,
, ,定义运算
,定义运算 ,则集合
,则集合 的子集的个数为( )
的子集的个数为( )
| A.3 | B.4 | C.8 | D.16 |
定义在 上的偶函数
上的偶函数 满足
满足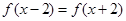 ,且在
,且在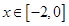 时,
时,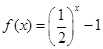 ,若关于
,若关于 的方程
的方程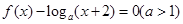 在
在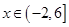 上恰有3个不同的实数解,则实数
上恰有3个不同的实数解,则实数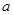 的取值范围为( )
的取值范围为( )
A.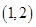 |
B. |
C. |
D. |
函数 的定义域为 .
的定义域为 .
已知 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时, ,则
,则 的值为 .
的值为 .
若 ,则
,则 .
.
函数 ,若
,若 在区间
在区间 上有零点,则实数
上有零点,则实数 的取值范围为 .
的取值范围为 .
(本大题满分10分)已知函数 ;
;
(1)求 的值;
的值;
(2)若 ,求
,求 的最大值和最小值.
的最大值和最小值.
(本大题满分12分)已知集合 ,
, ;
;
(1)若 ,求
,求 ;
;
(2)若 ,求实数
,求实数 的取值范围.
的取值范围.
(本大题满分12分)已知函数 ;
;
(1)求函数 的定义域;
的定义域;
(2)试判断函数 的奇偶性并证明;
的奇偶性并证明;
(3)若 ,求函数
,求函数 的值域.
的值域.
(本大题满分12分)如图所示,有一块半径为 的半圆形钢板,设计剪裁成矩形ABCD的形状,它的边
的半圆形钢板,设计剪裁成矩形ABCD的形状,它的边 在圆O的直径上,边CD的端点在圆周上,若设矩形的边
在圆O的直径上,边CD的端点在圆周上,若设矩形的边 为
为 ;
;
(1)将矩形的面积 表示为关于
表示为关于 的函数,并求其定义域;
的函数,并求其定义域;
(2)求矩形面积的最大值及此时边 的长度.
的长度.
(本大题满分12分)定义在 上的函数
上的函数 满足:①对任意
满足:①对任意 且
且 ,都有
,都有 成立; ②
成立; ② 在
在 上是奇函数,且
上是奇函数,且 .
.
(1)求证: 在
在 上是单调递增函数;
上是单调递增函数;
(2)解关于 不等式
不等式 ;
;
(3)若 对所有的
对所有的 及
及 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本大题满分12分)对于在区间 上有意义的两个函数
上有意义的两个函数 与
与 ,如果对任意的
,如果对任意的 ,均有
,均有 ,则称
,则称 与
与 在
在 上是接近的,否则称
上是接近的,否则称 与
与 在
在 上是非接近的.现在有两个函数
上是非接近的.现在有两个函数 与
与 ,现给定区间
,现给定区间 .
.
(1)若 ,判断
,判断 与
与 是否在给定区间上接近;
是否在给定区间上接近;
(2)若 与
与 在给定区间
在给定区间 上都有意义,求
上都有意义,求 的取值的集合
的取值的集合 ;
;
(3)在(2)的条件下,是否存在 ,使得
,使得 与
与 在给定区间
在给定区间 上是接近的;若存在,求
上是接近的;若存在,求 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.