直线 的倾斜角是
的倾斜角是 ,则
,则 的值是( )
的值是( )
| A.-1 | B.0 | C.1 | D.2 |
若 ,那么
,那么 =( )
=( )
A. |
B. |
C. |
D. |
若 ,则下列不等式成立的是( )
,则下列不等式成立的是( )
A. |
B. |
C. |
D. |
若直线
 :
: +
+ 与直线
与直线
 :
: 互相垂直,则
互相垂直,则 的值为( )
的值为( )
A. |
B. |
C. 或 或 |
D.1或 |
等比数列 的公比为
的公比为 ,若
,若 成等差数列.且
成等差数列.且 ,则
,则 ( )
( )
A. |
B.1 | C.2 | D.3 |
已知向量 ,若
,若 ,则
,则 的值是( )
的值是( )
A. |
B. |
C. |
D. |
若变量 满足约束条件
满足约束条件 则
则 的最大值为( )
的最大值为( )
| A.4 | B.3 | C.2 | D.1 |
过 的直线l与圆
的直线l与圆 交于A、B两点,当
交于A、B两点,当 面积最大时,直线的方程为( )
面积最大时,直线的方程为( )
A. B.
B.
C. D.
D.
如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M为线段PB的中点.有以下四个命题:
①PA∥平面MOB; ②OC⊥平面PAC;
③MO∥平面PAC; ④平面PAC⊥平面PBC.
其中正确的命题是( ).
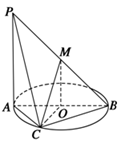
A.①② B.①③ C.③④ D.②④
公元前 世纪,古希腊欧几里得在《几何原本》里提出:“球的体积(
世纪,古希腊欧几里得在《几何原本》里提出:“球的体积( )与它的直径(
)与它的直径( )的立方成正比”,此即
)的立方成正比”,此即 ,欧几里得未给出
,欧几里得未给出 的值.
的值. 世纪日本数学家们对求球的体积的方法还不了解,他们将体积公式
世纪日本数学家们对求球的体积的方法还不了解,他们将体积公式 中的常数
中的常数 称为“立圆率”或“玉积率”.类似地,对于等边圆柱(轴截面是正方形的圆柱)、正方体也可利用公式
称为“立圆率”或“玉积率”.类似地,对于等边圆柱(轴截面是正方形的圆柱)、正方体也可利用公式 求体积(在等边圆柱中,
求体积(在等边圆柱中, 表示底面圆的直径;在正方体中,
表示底面圆的直径;在正方体中, 表示棱长).假设运用此体积公式求得球(直径为
表示棱长).假设运用此体积公式求得球(直径为 )、等边圆柱(底面圆的直径为
)、等边圆柱(底面圆的直径为 )、正方体(棱长为
)、正方体(棱长为 )的“玉积率”分别为
)的“玉积率”分别为 、
、 、
、 ,那么
,那么 ( )
( )
A. |
B. |
C. |
D. |
已知 为
为 内一点,满足
内一点,满足 ,
,  ,且
,且 ,则
,则 的面积为( )
的面积为( )
A. |
B. |
C. |
D. |
已知点 是圆C:
是圆C: 上的点,过点A且与圆C相交的直线AM、AN的倾斜角互补,则直线MN的斜率为( )
上的点,过点A且与圆C相交的直线AM、AN的倾斜角互补,则直线MN的斜率为( )
A. |
B. |
C. |
D.不为定值 |
不等式 的解集为
的解集为
已知点 在角
在角 的终边上,则
的终边上,则
已知圆C过点(0,1),且圆心在x轴负半轴上,直线l:y=x+1被该圆所截得的弦长为 ,则圆C的标准方程为________.
,则圆C的标准方程为________.
棱锥的三视图如图所示,且三个三角形均为直角三角形,则 的最小值为 .
的最小值为 .

(本题10分) 已知等差数列{ },
}, 为其前n项的和,
为其前n项的和, =0,
=0, =6,n∈N*.
=6,n∈N*.
(I)求数列{ }的通项公式;
}的通项公式;
(II)若 ,求数列{
,求数列{ }的前n项的和.
}的前n项的和.
(本小题满分12分)在锐角 中,
中, 分别是角
分别是角 所对的边,且
所对的边,且 .
.
(1)确定角 的大小;
的大小;
(2)若 ,且
,且 的面积为
的面积为 ,求
,求 的值.
的值.
(本小题满分12分)已知向量 函数
函数 。
。
(1)求函数 的最小正周期和最大值.
的最小正周期和最大值.
(2)求函数 的单调递增区间.
的单调递增区间.
(本小题满分12分)如图所示, 是正方形,
是正方形, ,
, 是
是 的中点.
的中点.
(1)求证: ;
;
(2)若 ,求三棱锥
,求三棱锥 的体积.
的体积.

(本小题满分12分)已知关于 的不等式
的不等式
(1)若不等式 的解集为
的解集为 ,求
,求 的值.
的值.
(2)求关于 的不等式
的不等式
 的解集
的解集
(本小题满分12分)已知圆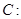
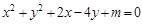 与
与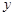 轴相切.
轴相切.
(1)求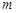 的值;
的值;
(2)若圆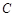 的切线在
的切线在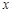 轴和
轴和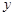 轴上的截距相等,求该切线方程;
轴上的截距相等,求该切线方程;
(3)从圆外一点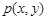 向圆引切线,M为切点,O为坐标原点,且有
向圆引切线,M为切点,O为坐标原点,且有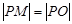 ,求使
,求使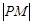 最小的点P的坐标.
最小的点P的坐标.