下列命题为真命题的是( )
A.若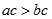 ,则 ,则 |
B.若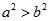 ,则 ,则 |
C.若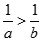 ,则 ,则 |
D.若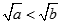 ,则 ,则 |
不等式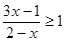 的解集是( )
的解集是( )
A.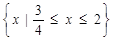 |
B.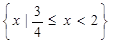 |
C.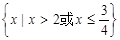 |
D.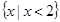 |
已知等差数列{an}满足a2+a4="4," a3+a5=10,则它的前10项的和S10=( )
| A.138 | B.135 | C.95 | D.23 |
若等比数列{an}的前n项和Sn,且S10=18,S20=24,则S40等于 ( )
A.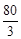 |
B. |
C.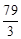 |
D.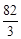 |
已知在△ABC中,三个内角A,B,C的对边分别为a,b,c,若△ABC的面积为S,且 ,则tanC等于 ( )
,则tanC等于 ( )
A.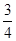 |
B.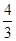 |
C.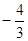 |
D. |
若两个等差数列 的前n项和分别为An、Bn,且满足
的前n项和分别为An、Bn,且满足 ,则
,则 的值为 ( )
的值为 ( )
A. |
B. |
C. |
D.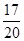 |
设 且
且 ,则( )
,则( )
A. |
B. |
C. |
D. |
若关于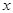 的方程
的方程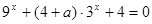 有解,则实数
有解,则实数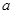 的取值范围是( )
的取值范围是( )
A. |
B.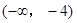 |
C. |
D. |
在数列{an}中,a1=2,an+1=an+ln(1+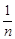 ),则an=( )
),则an=( )
| A.2+ln n | B.2+(n-1)ln n |
| C.2+n ln n | D.1+n+ln n |
设x,y满足约束条件 ,若目标函数
,若目标函数 的最大值为12,则
的最大值为12,则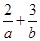 的最小值为 ( ).
的最小值为 ( ).
| A.4 | B. |
C. |
D. |
不等式ax2+4x+a>1-2x2对一切 恒成立,则实数a的取值范围是________
恒成立,则实数a的取值范围是________
在等差数列{an} 中,Sn是它的前n项和.若S16>0,且S17<0,则当Sn最大时n的值为________
实系数一元二次方程 有两个根,一个根在区间(0,1)内,另一个根在区间(1,2)内,则
有两个根,一个根在区间(0,1)内,另一个根在区间(1,2)内,则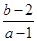 的取值范围________.
的取值范围________.
在数列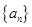 中,若前n项和
中,若前n项和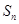 满足
满足 ,则该数列的通项公式
,则该数列的通项公式
下列命题成立的是 .(写出所有正确命题的序号).
①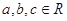 ,
,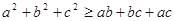 ;
;
②当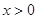 时,函数
时,函数 ,∴当且仅当
,∴当且仅当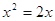 即
即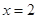 时
时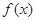 取最小值;
取最小值;
③当 时,
时, ;
;
④当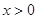 时,
时, 的最小值为
的最小值为
解关于x的不等式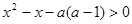
在锐角△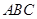 中,内角
中,内角 的对边分别为
的对边分别为 ,且
,且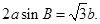
(1)求角 的大小。
的大小。
(2)若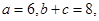 ,求△
,求△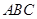 的面积。
的面积。
已知数列{an}的前n项和是Sn,且Sn+ an=1.
an=1.
(1)求数列{an}的通项公式;
(2)设bn=log3(1-Sn+1),求适合方程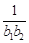 +
+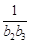 +…+
+…+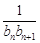 =
= 的n的值.
的n的值.
已知f(x)=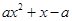 ,
,
(1)若函数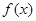 有最大值
有最大值 求实数
求实数 的值;
的值;
(2)若不等式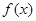 >
> 对一切实数
对一切实数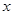 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围
某渔业公司年初用98万元购买一艘捕鱼船,第一年各种费用12万元,以后每年都增加4万元,每年捕鱼收益50万元.
(1)问第几年开始获利?
(2)若干年后,有两种处理方案:①年平均获利最大时,以26万元出售该渔船;②总纯收入获利最大时,以8万元出售该渔船.问哪种方案最合算?
(本小题14分)已知单调递增的等比数列{an}满足a2+a3+a4=28,且a3+2是a2,a4的等差中项.
(1)求数列{an}的通项公式;
(2)若bn= ,Sn=b1+b2+…+bn,对任意正整数n,Sn+(n+m)an+1<0恒成立,试求m的取值范围.
,Sn=b1+b2+…+bn,对任意正整数n,Sn+(n+m)an+1<0恒成立,试求m的取值范围.