若
，
，则一定有（ ）
A． |
B． |
C． |
D． |
下列不等式中，与不等式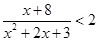
解集相同的是（ ）
A． |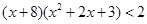
B． |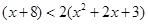
C． |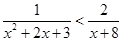
D． |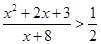
已知数列
满足：
，
，
，
，那么使
成立的n的最大值为（ ）
| A．4 | B．5 | C．24 | D．25 |
设
是等差数列，下列结论中正确的是（ ）
A．若 ，则 |
B．若 ，则 |
C．若 ，则 |
D．若 ，则 |
已知直线
，与
平行，则实数a的值是（ ）
| A．0或1 | B．1或 |
C．0或 |
D． |
圆
与圆
的位置关系为（ ）
| A．相交 | B．相切 | C．相离 | D．相交或相切 |
已知
，且
，若
恒成立，则实数m的取值范围是（ ）
A． |
B． |
C． |
D． |
已知不等式组
表示的平面区域为D，若函数
的图象上存在区域D上的点，则实数m的取值范围是（ ）
A． |
B． |
C． |
D． |
直线
与圆
的位置关系为（ ）
| A．相交 | B．相切 | C．相离 | D．相交或相切 |
已知实数
满足
，
，且
，则下列结论正确的是（ ）
A． |
B． |
C． |
D． |
已知数列
为等比数列，
为其前n项和，
，且
，
，则
．
直线
与直线
，直线
分别交于P、Q两点，PQ中点为
，则直线的斜率是 ．
已知数列
的前n项和为
，且有
，
，则
．
如果直线
和函数
的图象恒过同一个定点，且该定点始终落在圆
的内部或圆上，那么
的取值范围 ．
已知直线
与圆心为C的圆
相交于A、B两点，且
为等边三角形，则实数a= ．
已知数列
满足：
，当
时，
，若数列
满足对任意
，有
，则当时，
．
，
，
．
（1）比较
与
的大小；
（2）解关于x的不等式：
．
已知
为数列
的前n项和，且
，
．
（1）求数列的通项公式；
（2）设
，求数列
的前n项和
．
如图，
的顶点
，
的平分线CD所在直线方程为
，AC边上的高BH所在直线方程为
．
（1）求顶点C的坐标；
（2）求的面积．
已知圆
，点P是直线
上的一动点，过点P作圆M的切线PA，PB，切点为A，B．
（1）当切线PA的长度为
时，求点P的坐标；
（2）若
的外接圆为圆N，试问：当P在直线
上运动时，圆N是否过定点？若存在，求出所有的定点的坐标；若不存在，说明理由．
（3）求线段AB长度的最小值．