已知集合 ,
, ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
已知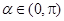 ,且
,且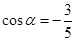 ,则
,则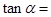 ( )
( )
A.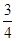 |
B.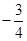 |
C.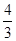 |
D.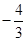 |
已知等差数列 的公差为
的公差为 ,若
,若 成等比数列,那么
成等比数列,那么 等于( )
等于( )
A. |
B. |
C. |
D. |
给出下列命题:
①若给定命题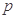 :
: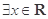 ,使得
,使得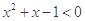 ,则
,则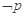 :
: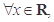 均有
均有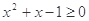 ;
;
②若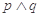 为假命题,则
为假命题,则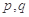 均为假命题;
均为假命题;
③命题“若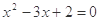 ,则
,则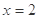 ”的否命题为“若
”的否命题为“若 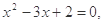 则
则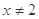
其中正确的命题序号是( )
| A.① | B.①② | C.①③ | D.②③ |
已知函数 的图象(部分)如图所示,则
的图象(部分)如图所示,则 的解析式是( )
的解析式是( )

A. |
B. |
C. |
D. |
设p: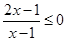 ,q:
,q: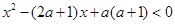 ,若p是q的充分不必要条件,则实数
,若p是q的充分不必要条件,则实数 的取值范围是( )
的取值范围是( )
A.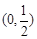 |
B.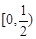 |
C. |
D. |
在 中,已知
中,已知 ,
, ,
, 分别是
分别是 边上的三等分点,则
边上的三等分点,则 的值是( )
的值是( )
A. |
B. |
C. |
D. |
已知定义在R上的函数 且
且 .若方程
.若方程 有三个不相等的实数根,则实数k的取值范围是( )
有三个不相等的实数根,则实数k的取值范围是( )
A. |
B. |
C. |
D. |
已知三个数 ,其中最大的数是 .
,其中最大的数是 .
已知平面向量 .若向量
.若向量 ,则实数
,则实数 的值是 .
的值是 .
如图,在 中,
中, 是
是 中点,
中点, ,则
,则 .
.

若函数 (
( )是偶函数,则
)是偶函数,则 的最小值为 .
的最小值为 .
若函数 在区间
在区间 上单调递增,则实数
上单调递增,则实数 的取值范围是 .
的取值范围是 .
如图,已知边长为4的正方形ABCD,E是BC边上一动点(与B、C不重合),连结AE,作EF⊥AE交∠BCD的外角平分线于F.设 ,记
,记 ,则函数
,则函数 的值域是 ;当
的值域是 ;当 面积最大时,
面积最大时, .
.

已知函数 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求函数 的单调递减区间及对称轴方程.
的单调递减区间及对称轴方程.
已知等差数列 的首项
的首项 ,公差
,公差 ,前
,前 项和为
项和为 ,且
,且 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)求证: .
.
在 中,角
中,角 所对的边分别为
所对的边分别为 .且
.且 .[来源
.[来源
(Ⅰ)若 ,求角
,求角 ;
;
(Ⅱ)求 的取值范围.
的取值范围.
已知函数 .
.
(Ⅰ)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅱ)当 时,证明
时,证明 .
.
已知函数 (其中
(其中 是常数,
是常数, ,
, ),函数
),函数 的导函数为
的导函数为 ,且
,且 .
.
(Ⅰ)若 ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)当 时,若函数
时,若函数 在区间
在区间 上的最大值为
上的最大值为 ,试求
,试求 的值.
的值.
已知实数数列 满足:
满足: ,
, ,记集合
,记集合
(Ⅰ)若 ,用列举法写出集合
,用列举法写出集合 ;
;
(Ⅱ)若 ,判断数列
,判断数列 是否为周期数列,并说明理由;
是否为周期数列,并说明理由;
(Ⅲ)若 ,且
,且 ,求集合
,求集合 的元素个数的最小值.
的元素个数的最小值.