已知集合 ,集合
,集合 ,集合
,集合 .则集合
.则集合 可表示为
可表示为
A.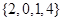 |
B. |
C. |
D. |
复数 满足
满足 (其中
(其中 为虚数单位),则
为虚数单位),则 =
=
A. |
B. |
C. |
D. |
下列函数中,为奇函数的是
A. |
B.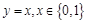 |
C. |
D. |
下面几种推理中是演绎推理的为
| A.由金、银、铜、铁可导电,猜想:金属都可导电; |
B.猜想数列 的通项公式为 的通项公式为  ; ; |
C.半径为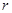 圆的面积 圆的面积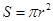 ,则单位圆的面积 ,则单位圆的面积 ; ; |
D.由平面直角坐标系中圆的方程为 ,推测空间直角坐标系中球的方程为 ,推测空间直角坐标系中球的方程为 |
已知 ,若
,若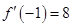 ,则
,则
| A.4 | B.5 | C. |
D. |
“ ”是“ 函数
”是“ 函数 在区间
在区间 上单调递减”的
上单调递减”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
如图1,在矩形 内:记抛物线
内:记抛物线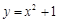 与直线
与直线 围成的区域为
围成的区域为 (图中阴影部分).则区域M面积与矩形
(图中阴影部分).则区域M面积与矩形 面积之比为
面积之比为
A. |
B. |
C.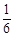 |
D. |
已知可导函数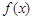
 满足
满足 ,则当
,则当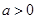 时,
时, 和
和 大小关系为
大小关系为
A.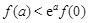 |
B. |
C.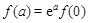 |
D.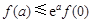 |
函数 的定义域为 .
的定义域为 .
某几何体的三视图如图所示,其正视图是边长为2的正方形,侧视图和俯视图都是等腰直角三角形,则此几何体的体积是 .

已知双曲线 与椭圆
与椭圆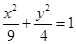 有相同的焦点,且双曲线
有相同的焦点,且双曲线 的渐近线方程为
的渐近线方程为 ,则双曲线
,则双曲线 的方程为 .
的方程为 .
设实数 满足
满足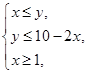 向量
向量 ,
,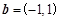 .若
.若 ,则实数
,则实数 的最大值为 .
的最大值为 .
在数列 中,已知
中,已知 ,
, 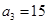 ,且数列
,且数列 是等比数列,则
是等比数列,则 .
.
已知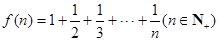 ,且
,且 ,推测当
,推测当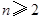 时,有____.
时,有____.
已知函数 的图像经过点
的图像经过点 .
.
(1)求 的值;
的值;
(2)在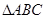 中,
中, 、
、 、
、 所对的边分别为
所对的边分别为 、
、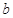 、
、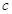 ,若
,若 ,且
,且 .求
.求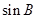 .
.
已知数列 的前
的前 项和
项和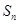 满足:
满足: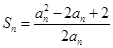 ,且
,且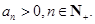
(1)求
(2)猜想 的通项公式,并用数学归纳法证明
的通项公式,并用数学归纳法证明
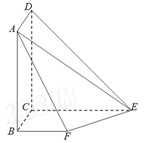
如图所示,平面
 平面
平面 ,且四边形
,且四边形 为矩形,四边形
为矩形,四边形 为直角梯形,
为直角梯形,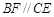 ,
,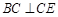 ,
,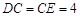 ,
,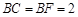 .
.
(1)求证
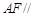 平面
平面 ;
;
(2)求平面 与平面
与平面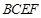 所成锐二面角的余弦值;
所成锐二面角的余弦值;
(3)求直线 与平面
与平面 所成角的余弦值.
所成角的余弦值.
已知数列 的前
的前 项和为
项和为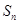 ,且满足
,且满足 .
.
(1)求 ,
, 的值;
的值;
(2)求 ;
;
(3)设 ,数列
,数列 的前
的前 项和为
项和为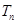 ,求证:
,求证: .
.
设双曲线C: (a>0,b>0)的一个焦点坐标为(
(a>0,b>0)的一个焦点坐标为( ,0),离心率
,0),离心率 , A、B是双曲线上的两点,AB的中点M(1,2).
, A、B是双曲线上的两点,AB的中点M(1,2).
(1)求双曲线C的方程;
(2)求直线AB方程;
(3)如果线段AB的垂直平分线与双曲线交于C、D两点,那么A、B、C、D四点是否共圆?为什么?
设函数 .
.
(1)若函数 在区间(-2,0)内恰有两个零点,求a的取值范围;
在区间(-2,0)内恰有两个零点,求a的取值范围;
(2)当a=1时,求函数 在区间[t,t+3]上的最大值.
在区间[t,t+3]上的最大值.