已知集合 ,
, ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
命题“若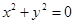 ,则
,则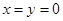 ”的否命题为( )
”的否命题为( )
A.若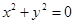 ,则 ,则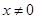 且 且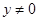 |
B.若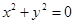 ,则 ,则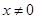 或 或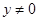 |
C.若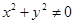 ,则 ,则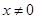 且 且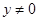 |
D.若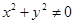 ,则 ,则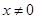 或 或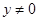 |
欧拉公式 (
( 为虚数单位)是由瑞士著名数学家欧拉发明的,它将指数函数的定义域扩大到复数,建立了三角函数和指数函数的关系,它在复变函数论里占有非常重要的地位,被誉为“数学中的天桥”,根据欧拉公式可知,
为虚数单位)是由瑞士著名数学家欧拉发明的,它将指数函数的定义域扩大到复数,建立了三角函数和指数函数的关系,它在复变函数论里占有非常重要的地位,被誉为“数学中的天桥”,根据欧拉公式可知, 表示的复数在复平面中位于( )
表示的复数在复平面中位于( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
函数 则
则 ( )
( )
A. |
B. |
C. |
D. |
等差数列 前
前 项和为
项和为 ,且
,且 ,则数列
,则数列 的公差为( )
的公差为( )
| A.1 | B.2 | C.2015 | D.2016 |
若 ,
, ,
, ,则
,则 的大小关系( )
的大小关系( )
A. |
B. |
C. |
D. |
已知 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
已知某几何体的三视图的侧视图是一个正三角形,如图所示,则该几何体的体积等于( )

A. |
B. |
C. |
D. |
已知函数 ,
, 的周期为
的周期为 ,若将其图象沿
,若将其图象沿 轴向右平移
轴向右平移 个单位
个单位 ,所得图象关于原点对称,则实数
,所得图象关于原点对称,则实数 的最小值为( )
的最小值为( )
A. |
B. |
C. |
D. |
如图所示,在正六边形 中,点
中,点 是
是 内(包括边界)的一个动点,设
内(包括边界)的一个动点,设 ,则
,则 的取值范围是( )
的取值范围是( )

A. |
B. |
C. |
D. |
若一个四棱锥底面为正方形,顶点在底面的射影为正方形的中心,且该四棱锥的体积为9,当其外接球表面积最小时,它的高为( )
| A.3 | B. |
C. |
D. |
关于函数 ,下列说法错误的是( )
,下列说法错误的是( )
A. 是 是 的极小值点 的极小值点 |
B.函数 有且只有1个零点 有且只有1个零点 |
C.存在正实数 ,使得 ,使得 恒成立 恒成立 |
D.对任意两个正实数 ,且 ,且 ,若 ,若 ,则 ,则 |
已知平面直角坐标系中, ,
, ,则向量
,则向量 在向量
在向量 的方向上的投影是 .
的方向上的投影是 .
若函数 ,
, 为偶函数,则实数
为偶函数,则实数 .
.
设实数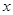 ,
, 满足约束条件
满足约束条件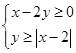 ,则
,则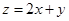 的最大值为 .
的最大值为 .
如图所示,已知 中,
中, ,
, ,
, ,
, 为边
为边 上的一点,
上的一点, 为
为 上的一点,且
上的一点,且 ,则
,则 .
.

在等比数列 中,
中, ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,且
,且 为递增数列,若
为递增数列,若 ,求证:
,求证: .
.
如图, 中,三个内角
中,三个内角 、
、 、
、 成等差数列,且
成等差数列,且 ,
, .
.
(1)求 的面积;
的面积;
(2)已知平面直角坐标系 ,点
,点 ,若函数
,若函数
 的图象经过
的图象经过 、
、 、
、 三点,且
三点,且 、
、 为
为 的图象与
的图象与 轴相邻的两个交点,求
轴相邻的两个交点,求 的解析式.
的解析式.
如图,已知长方形 中,
中, ,
, ,
, 为
为 的中点.将
的中点.将 沿
沿 折起,使得平面
折起,使得平面 平面
平面 .
.
(1)求证: ;
;
(2)若点 是线段
是线段 上的一动点,问点
上的一动点,问点 在何位置时,二面角
在何位置时,二面角 的余弦值为
的余弦值为 .
.
小明同学制作了一个简易的网球发射器,可用于帮忙练习定点接发球,如图1所示,网球场前半区、后半区总长为23.77米,球网的中间部分高度为0.914米,发射器固定安装在后半区离球网底部8米处中轴线上,发射方向与球网底部所在直线垂直.为计算方便,球场长度和球网中间高度分别按24米和1米计算,发射器和网球大小均忽略不计.如图2所示,以发射器所在位置为坐标原点建立平面直角坐标系 ,
, 轴在地平面上的球场中轴线上,
轴在地平面上的球场中轴线上, 轴垂直于地平面,单位长度为1米.已知若不考虑球网的影响,网球发射后的轨迹在方程
轴垂直于地平面,单位长度为1米.已知若不考虑球网的影响,网球发射后的轨迹在方程 表示的曲线上,其中
表示的曲线上,其中 与发射方向有关.发射器的射程是指网球落地点的横坐标.
与发射方向有关.发射器的射程是指网球落地点的横坐标.


(1)求发射器的最大射程;
(2)请计算 在什么范围内,发射器能将球发过网(即网球飞行到球网正上空时,网球离地距离大于1米)?若发射器将网球发过球网后,在网球着地前,小明要想在前半区中轴线的正上空选择一个离地面2.55米处的击球点正好击中网球,试问击球点的横坐标
在什么范围内,发射器能将球发过网(即网球飞行到球网正上空时,网球离地距离大于1米)?若发射器将网球发过球网后,在网球着地前,小明要想在前半区中轴线的正上空选择一个离地面2.55米处的击球点正好击中网球,试问击球点的横坐标 最大为多少?并请说明理由.
最大为多少?并请说明理由.
已知函数 .
.
(1)若直线 与
与 的反函数的图象相切,求实数
的反函数的图象相切,求实数 的值;
的值;
(2)设 ,且
,且 ,
, ,
, ,
, ,试比较
,试比较 三者的大小,并说明理由.
三者的大小,并说明理由.
选修4-1 几何证明选讲
如图, 是圆
是圆 的直径,点
的直径,点 在弧
在弧 上,点
上,点 为弧
为弧 的中点,作
的中点,作 于点
于点 ,
, 与
与 交于点
交于点 ,
, 与
与 交于点
交于点 .
.
(1)证明: ;
;
(2)若 ,
, ,求圆
,求圆 的半径.
的半径.
选修4-4 极坐标与参数方程
已知曲线 的极坐标方程为
的极坐标方程为 ,将曲线
,将曲线 (
( 为参数)经过伸缩变换
为参数)经过伸缩变换 后得到曲线
后得到曲线 .
.
(1)求曲线 的参数方程;
的参数方程;
(2)若点 在曲线
在曲线 上运动,试求出
上运动,试求出 到曲线
到曲线 的距离的最小值.
的距离的最小值.
选修4-5 不等式证明选讲
已知函数 ,且满足
,且满足
 的解集不是空集.
的解集不是空集.
(1)求实数 的取值集合
的取值集合 ;
;
(2)若 ,求证:
,求证: .
.