设全集 ,则下图中阴影部分表示的集合为( )
,则下图中阴影部分表示的集合为( )

A. |
B. |
C. |
D. |
已知复数 ,则其共轭复数
,则其共轭复数 在复平面上对应的点位于( )
在复平面上对应的点位于( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
“ ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
下列函数中,在区间 上是减函数的是( )
上是减函数的是( )
A. |
B. |
C. |
D. |
等比数列 的公比为2,且
的公比为2,且 ,则
,则 =( )
=( )
| A.1 | B.-1 | C. |
D. |
已知 ,且
,且 与
与 垂直,则
垂直,则 =( )
=( )
A. |
B. |
C. |
D. |
函数 的大致图像是( )
的大致图像是( )

若实数 满足不等式组
满足不等式组 ,则
,则 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
若一个几何体的三视图如图所示,则该几何体的表面积为( )

A. |
B. |
C. |
D. |
若 ,且函数
,且函数 在
在 处有极值,则
处有极值,则 的最小值为( )
的最小值为( )
A. |
B. |
C. |
D. |
在 中,若
中,若 ,三角形的面积
,三角形的面积 ,则三角形外接圆的半径为( )
,则三角形外接圆的半径为( )
A. |
B.2 | C. |
D.4 |
对实数 和
和 定义运算“
定义运算“ ”:
”: 设函数
设函数 ,若函数
,若函数 恰有两个不同的零点,则实数
恰有两个不同的零点,则实数 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
已知 ,且
,且 ,则
,则 =__________.
=__________.
已知数列满足 ,且
,且 =2,则
=2,则 =__________.
=__________.
已知平面三角形和空间四面体有很多相似的性质,请你类比三角形的面积公式 (其中
(其中 、
、 、
、 是三角形的三条边,
是三角形的三条边, 是三角形内切圆的半径),写出一个关于四面体的与之类似的结论________________________.
是三角形内切圆的半径),写出一个关于四面体的与之类似的结论________________________.
若对于一切实数 ,不等式
,不等式 恒成立,则
恒成立,则 的取值范围是_____.
的取值范围是_____.
已知等比数列 中
中 ,数列
,数列 满足
满足 .
.
(1)求数列 和
和 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
已知数列 的前
的前 项和为
项和为 .
.
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和 的取值范围.
的取值范围.
已知函数 的最大值为3,函数
的最大值为3,函数 的图象上相邻两对称轴间的距离为
的图象上相邻两对称轴间的距离为 ,且
,且 .
.
(1)求函数 的解析式;
的解析式;
(2)将 的图象向左平移
的图象向左平移 个单位,再向下平移1个单位后得到函数
个单位,再向下平移1个单位后得到函数 的图象,试判断
的图象,试判断 的奇偶性,并求出
的奇偶性,并求出 在R上的单调递增区间.
在R上的单调递增区间.
设函数 .
.
(1)求 的最大值,并写出使
的最大值,并写出使 取最大值时
取最大值时 的集合;
的集合;
(2)已知 中,角
中,角 的对边分别为
的对边分别为 ,若
,若 ,
, ,求
,求 的最小值.
的最小值.
已知函数 ,
,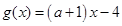 .
.
(1)当 时,求函数
时,求函数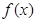 在
在 处的切线方程;
处的切线方程;
(2)是否存在实数 ,使得对任意的
,使得对任意的 ,恒有
,恒有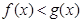 成立?若存在,求出实数
成立?若存在,求出实数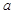 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
在直角坐标系中,以原点为极点, 轴的正半轴为极轴建立坐标系,已知曲线
轴的正半轴为极轴建立坐标系,已知曲线 ,过点
,过点 的直线
的直线 (
( 为参数)与曲线
为参数)与曲线 相交于M,N两点.
相交于M,N两点.
(1)求曲线 和直线
和直线 的普通方程;
的普通方程;
(2)若 、
、 、
、 成等比数列,求实数
成等比数列,求实数 的值.
的值.