直线
为参数）的倾斜角为 （ ）
A． |
B． |
C． |
D． |
双曲线
的焦点到渐近线的距离为（ ）
A． |
B．2 | C． |
D． |
方程
表示的圆（ ）
| A．关于x轴对称 |
| B．关于y轴对称 |
C．关于直线 对称 |
D．关于直线 对称 |
两圆
与
的位置关系是（ ）
| A．相离 | B．相交 | C．外切 | D．内切 |
当
时，曲线
与曲线
有相同的（ ）
| A．焦点 | B．准线 | C．焦距 | D．离心率 |
若过点
的直线与圆
有公共点，则该直线的倾斜角的取值范围是（ ）
A． |
B． |
C． |
D． |
若双曲线
与直线
无公共点，则离心率
的取值范围是（ ）
A． |
B． |
C． |
D． |
若椭圆的中心在原点，一个焦点为
，直线
与椭圆相交所得弦的中点的纵坐标
为1，则这个椭圆的方程为（ ）
A． |
B． |
C． |
D． |
与圆
和圆
都相切的圆的圆心轨迹是（ ）
| A．椭圆 |
| B．椭圆和双曲线的一支 |
| C．双曲线和一条直线（去掉几个点） |
| D．双曲线的一支和一条直线（去掉几个点） |
过抛物线
的焦点F作斜率为1的直线，交抛物线于A、B两点，若
，
则
等于（ ）
A．
B．
C．
D．
若所有满足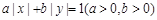
的实数x, y均满足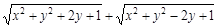
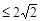，则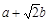
的取值范围为（ ）
A． |
B． |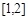
C． |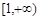
D． |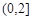
如图，在等腰梯形ABCD中，AB∥CD，且AB=2AD，设
，
，以A、B为焦点且过点D的双曲线的离心率为
，以C、D为焦点且过点A的椭圆的离心率为
，则
（ ）
A．随着
角的增大而增大 B．随着角的增大而减小
C．为定值1 D．为定值2
在极坐标系中，经过点
且与极轴垂直的直线的极坐标方程为 ．
在平面直角坐标系中，已知△ABC顶点
和
，顶点B在椭圆
上，则
．
直角△ABC的三个顶点都在给定的抛物线
上，且斜边AB和y轴平行，则△ABC斜边上的高的长度为 ．
已知椭圆
的右焦点为
，设A，B为椭圆上关于原点对称的两点，AF的中点为M，BF的中点为N，原点O在以线段MN为直径的圆上．若直线AB的斜率k满足
，则椭圆离心率
的取值范围为 ．
求与直线
相切于点（3, 4），且在y轴上截得的弦长为
的圆的方程．
已知在直角坐标系
中，曲线
为参数，
，在以O为极点，x轴
正半轴为极轴的极坐标系中，曲线
，曲线
．
（Ⅰ）求C2与C3交点的直角坐标；
（Ⅱ）若C2与C1相交于点A，C3与C1相交于点B，求
的值．
为捍卫钓鱼岛及其附属岛屿的领土主权，中国派出海警“2102”、“海警2307”和“海警2308”海警船编队在钓鱼岛领海巡航。某日，正巡逻在A处的海警“2102”突然发现来自P处的疑似敌舰的某信号，发现信号时“海警2307”和“海警2308”正分别位于如图所示的B、C两处，其中
在
的正东方向相距
千米处，
在的北偏西30°方向相距
千米处。由于、比距
更远，因此，4秒后、才同时发现这一信号（该信号的传播速度为每秒
千米），试确定疑似敌舰相对于A的位置．
已知动点P与两定点
、
连线的斜率之积为
（Ⅰ）求动点P的轨迹C的方程；
（Ⅱ）若过点
的直线l交轨迹C于M、N两点，且轨迹C上存在点E使得四边形OMEN（O为坐标原点）为平行四边形，求直线l的方程．
已知M为抛物线
上一动点，
为其对称轴上一点，直线MA与抛物线的另一个交点为N．当A为抛物线的焦点且直线MA与其对称轴垂直时，△OMN的面积为
．
（Ⅰ）求抛物线的标准方程；
（Ⅱ）记
，若t的值与M点位置无关， 则称此时的点A为“稳定点”，试求出所有“稳定点”，若没有，请说明理由．
已知椭圆
的离心率为
，左、右焦点分别为E、F，椭圆上的点P满足
，且△PEF的面积为1，抛物线
经过点（2，2）．
（Ⅰ）分别求椭圆与抛物线的方程；
（Ⅱ）已知
为
轴上一点，倾斜角为
的直线
交椭圆于A、B两点，线段AB的中点为M，直线QM交抛物线于C、D两点，四边形ACBD的面积记为S，若对任意直线l，都存在点Q，使得
，求实数
的取值范围．