已知集合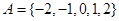 ,
,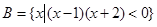 ,则
,则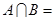 ( )
( )
| A.{-1,0} | B.{0,1} | C.{-1,0,1} | D.{0,1,2} |
已知函数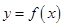 在
在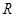 上的图像是连续不断的一条曲线, 在用二分法研究函数
上的图像是连续不断的一条曲线, 在用二分法研究函数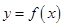 的零点时, 第一次计算得到数据:
的零点时, 第一次计算得到数据: ,根据零点的存在性定理知存在零点
,根据零点的存在性定理知存在零点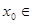 , 第二次计算 , 以上横线处应填的内容为( )
, 第二次计算 , 以上横线处应填的内容为( )
A.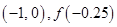 |
B.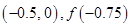 |
C.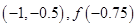 |
D.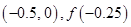 |
设集合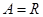 ,集合
,集合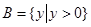 ,下列对应关系中是从集合
,下列对应关系中是从集合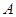 到集合
到集合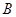 的映射的是( )
的映射的是( )
A.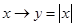 |
B.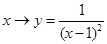 |
C. |
D.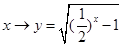 |
函数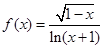 的定义域为( )
的定义域为( )
A.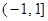 |
B.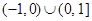 |
C.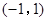 |
D.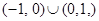 |
方程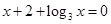 的根所在的区间为( )
的根所在的区间为( )
A. |
B. |
C.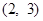 |
D.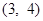 |
函数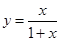 的图像是( )
的图像是( )
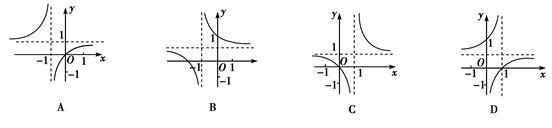
在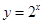 ,
,  ,
, 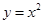 这三个函数中,当
这三个函数中,当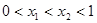 时,使
时,使
 恒成立的函数的个数是 ( )
恒成立的函数的个数是 ( )
A.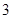 个 个 |
B. 个 个 |
C.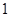 个 个 |
D. 个 个 |
已知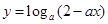 在
在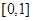 上是关于
上是关于 的减函数,则实数
的减函数,则实数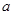 的取值范围是( )
的取值范围是( )
A.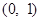 |
B. |
C. |
D. |
如图所示的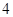 个图象中,与所给3件事吻合最好的顺序 (其中
个图象中,与所给3件事吻合最好的顺序 (其中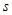 表示离开家的距离,
表示离开家的距离,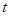 表示离开家的时间)为( )
表示离开家的时间)为( )
① 我离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学;
② 我骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;
③ 我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.
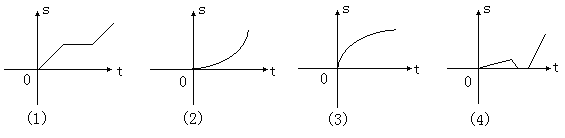
| A.(1)(2)(4) | B.(4)(1)(3) | C.(1)(2)(3) | D.(4)(1)(2) |
若关于 的方程
的方程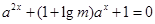
 且
且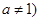 有实数解,则实数
有实数解,则实数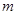 的取值范围是( )
的取值范围是( )
A.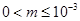 或 或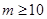 |
B.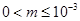 |
C.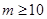 |
D. |
已知函数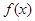 是定义在
是定义在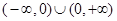 上的奇函数, 在区间
上的奇函数, 在区间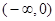 单调递增且
单调递增且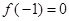 .若实数
.若实数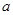 满足
满足 , 则实数
, 则实数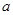 的取值范围是( )
的取值范围是( )
A.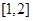 |
B. |
C.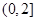 |
D. |
已知函数
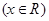 ,则使方程
,则使方程
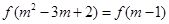 成立的整数
成立的整数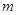 的个数是( )
的个数是( )
| A.3个 | B.4个 | C.5个 | D.无穷多个 |
已知函数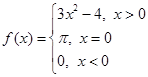 ,则
,则 = .
= .
若幂函数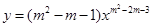 在
在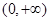 上是减函数,则实数
上是减函数,则实数 的值为 .
的值为 .
实数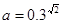 ,
,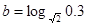 ,
,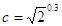 ,则实数
,则实数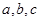 的大小关系为 .
的大小关系为 .
设函数 ,那么函数
,那么函数 的零点的个数为 .
的零点的个数为 .
已知实数集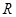 ,集合
,集合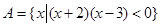 ,集合
,集合
(Ⅰ)当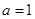 时,求
时,求 ;
;
(Ⅱ)设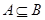 ,求实数
,求实数 的取值范围.
的取值范围.
某自来水厂的蓄水池有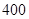 吨水,水厂每小时可向蓄水池中注水
吨水,水厂每小时可向蓄水池中注水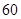 吨,同时蓄水池又向居民小区不间断供水,
吨,同时蓄水池又向居民小区不间断供水,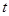 小时内供水总量为
小时内供水总量为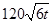 吨,其中
吨,其中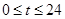 .
.
(Ⅰ)从供水开始到第几小时,蓄水池中的存水量最少? 最少水量是多少吨?
(Ⅱ)若蓄水池中水量少于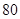 吨时,就会出现供水紧张现象,请问:在一天的
吨时,就会出现供水紧张现象,请问:在一天的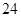 小时内,大约有几小时出现供水紧张现象?
小时内,大约有几小时出现供水紧张现象?
记 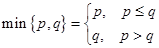 , 若函数
, 若函数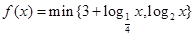 .
.
(Ⅰ)用分段函数形式写出函数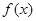 的解析式;
的解析式;
(Ⅱ)求不等式 的解集.
的解集.
已知函数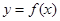 的定义域为
的定义域为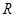 ,且对任意实数
,且对任意实数 恒有
恒有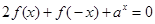
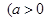 且
且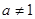 )成立.
)成立.
(Ⅰ)求函数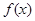 的解析式;
的解析式;
(Ⅱ)讨论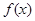 在
在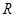 上的单调性, 并用定义加以证明.
上的单调性, 并用定义加以证明.
已知函数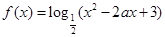 .
.
(Ⅰ)若函数 的定义域为
的定义域为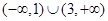 ,求实数
,求实数 的值;
的值;
(Ⅱ)若函数 的定义域为
的定义域为 ,值域为
,值域为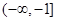 ,求实数
,求实数 的值;
的值;
(Ⅲ)若函数 在
在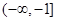 上为增函数, 求实数
上为增函数, 求实数 的取值范围.
的取值范围.
设函数 (
(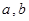 为实常数).
为实常数).
(Ⅰ)当 时,证明:函数
时,证明:函数 不是奇函数;
不是奇函数;
(Ⅱ)设函数 是实数集
是实数集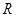 上的奇函数,求
上的奇函数,求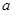 与
与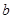 的值;
的值;
(Ⅲ)当 为奇函数时,设其定义域为
为奇函数时,设其定义域为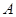 ,是否存在同时满足下列两个条件的区间
,是否存在同时满足下列两个条件的区间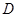 :(1)
:(1)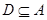 ,(2)对任何
,(2)对任何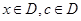 ,都有
,都有 成立? 若存在,求出这样的区间
成立? 若存在,求出这样的区间 ;若不存在,请说明理由.
;若不存在,请说明理由.