如果 ,那么正确的结论是
,那么正确的结论是
A. |
B. |
C. |
D. |
函数 的定义域是
的定义域是
A. |
B. |
C. |
D. |
已知全集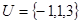 ,集合
,集合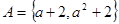 ,且
,且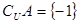 ,则
,则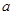 的值是
的值是
A.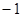 |
B.1 | C.3 | D.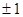 |
函数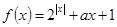 为偶函数,则
为偶函数,则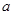 等于
等于
A.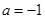 |
B.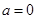 |
C.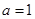 |
D.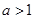 |
设 ,则
,则 的大小关系是
的大小关系是
A. |
B. |
C. |
D. |
根据统计,一名工人组装第 件产品所用的时间(单位:分钟)为
件产品所用的时间(单位:分钟)为 (
( 为常数).已知工人组装第4件产品用时30分钟,组装第
为常数).已知工人组装第4件产品用时30分钟,组装第 件产品用时5分钟,那么
件产品用时5分钟,那么 和
和 的值分别是
的值分别是
| A.75,25 | B.75,16 | C.60,144 | D.60,16 |
函数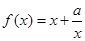 的图像不可能是
的图像不可能是 
函数 的单调递增区间为
的单调递增区间为
A. |
B. |
C. |
D. |
对于函数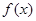 定义域中任意的
定义域中任意的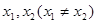 有如下结论
有如下结论
①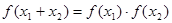
②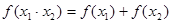
③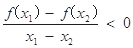
④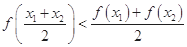
当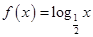 时,上述结论中正确的序号是
时,上述结论中正确的序号是
| A.①③ | B.②③ | C.②④ | D.②③④ |
设函数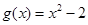 ,
,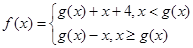 ,则
,则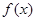 的值域是
的值域是
A.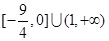 |
B.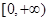 |
C.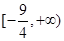 |
D.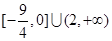 |
已知集合 ,
, ,若A=B,则a+b=_______.
,若A=B,则a+b=_______.
当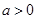 且
且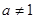 时,函数
时,函数 必过定点_______.
必过定点_______.
若对数函数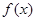 与幂函数
与幂函数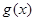 的图象相交于一点
的图象相交于一点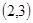 ,则
,则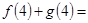 .
.
方程 有两个不相等的实数根,则
有两个不相等的实数根,则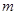 的取值范围是 .
的取值范围是 .
已知 是奇函数,且
是奇函数,且 ,若
,若 ,则
,则 .
.
若函数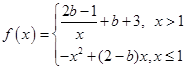 在
在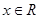 内满足:对于任意的实数
内满足:对于任意的实数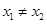 ,都有
,都有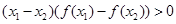 成立,则实数
成立,则实数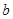 的取值范围为 .
的取值范围为 .
 表示不超过
表示不超过 的最大整数,定义函数
的最大整数,定义函数 .则下列结论中正确的有 .
.则下列结论中正确的有 .
①函数 的值域为
的值域为
②方程 有无数个解
有无数个解
③函数 的图像是一条直线
的图像是一条直线
④函数 是
是 上的增函数
上的增函数
不用计算器求下列各式的值:
(1) ;
;
(2) .
.
设集合 ,B={x|
,B={x| <1},
<1}, .
.
(1)求 ;
;
(2)若 ,求
,求 的取值范围.
的取值范围.
已知函数
 (
( 是常数),且
是常数),且 ,
, .
.
(1)求 的值;
的值;
(2)当 时,判断
时,判断 的单调性并用定义证明;
的单调性并用定义证明;
(3)若不等式 成立,求实数
成立,求实数 的取值范围.
的取值范围.
已知 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,函数的解析式为
时,函数的解析式为 .
.
(1)写出 在
在 上的解析式;
上的解析式;
(2)求 在
在 上的最大值.
上的最大值.
(3)对任意的 都有
都有 成立,求最小的整数M的值.
成立,求最小的整数M的值.
已知函数 .
.
(Ⅰ)当 时,证明:
时,证明: 为奇函数;
为奇函数;
(Ⅱ)若关于 的方程
的方程 有两个不等实数根,求实数
有两个不等实数根,求实数 的取值范围.
的取值范围.