已知集合P {
{ |
| -
- ≤0},M
≤0},M {0,1,3,4},则集合
{0,1,3,4},则集合 中元素的个数为( )
中元素的个数为( )
| A.1 | B.2 | C.3 | D.4 |
下列函数中为偶函数的是( )
A. |
B. |
C. |
D. |
在 中,∠A
中,∠A 60°,|
60°,| |
| 2,|
2,| |
| 1,则
1,则 的值为( )
的值为( )
A. |
B. |
C.1 | D. |
数列{ }的前
}的前 项和
项和 ,若
,若 -
- 2
2 -1(
-1( ≥2),且
≥2),且 3,则
3,则 1的值为( )
1的值为( )
| A.0 | B.1 | C.3 | D.5 |
已知函数 ,下列结论中错误的是( )
,下列结论中错误的是( )
A. |
B. 的最小正周期为 的最小正周期为 |
C. 的图像关于直线 的图像关于直线 对称 对称 |
D. 的值域为 的值域为 |
“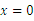 ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
如图,点O为坐标原点,点A(1,1).若函数 (
( >0,且
>0,且 ≠1)及
≠1)及 (
( ,且
,且 ≠1)的图象与线段OA分别交于点M,N,且M,N恰好是线段OA的两个三等分点,则
≠1)的图象与线段OA分别交于点M,N,且M,N恰好是线段OA的两个三等分点,则 ,
, 满足( )
满足( )

A. |
B. |
C. |
D. |
已知函数 ,函数
,函数 .若函数
.若函数 恰好有2个不同的零点,则实数
恰好有2个不同的零点,则实数 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
函数 的定义域为_____.
的定义域为_____.
若角 的终边过点(1,-2),则
的终边过点(1,-2),则 =_____.
=_____.
若等差数列 满足
满足 ,
, ,则
,则 = ______.
= ______.
已知向量 ,点
,点 ,点
,点 为直线
为直线 上一个动点.若
上一个动点.若 //
// ,则点
,则点 的坐标为____.
的坐标为____.
已知函数 .若
.若 的图像向左平移
的图像向左平移 个单位所得的图像与
个单位所得的图像与 的图像重合,则
的图像重合,则 的最小值为____.
的最小值为____.
对于数列 ,若
,若 ,
, ,均有
,均有 ,则称数列
,则称数列 具有性质
具有性质 .
.
(1)若数列 的通项公式为
的通项公式为 ,且具有性质
,且具有性质 ,则
,则 的最大值为____;
的最大值为____;
(2)若数列 的通项公式为
的通项公式为 ,且具有性质
,且具有性质 ,则实数
,则实数 的取值范围是____.
的取值范围是____.
已知等比数列 的公比
的公比 ,且
,且 ,
, .
.
(Ⅰ)求公比 和
和 的值;
的值;
(Ⅱ)若 的前
的前 项和为
项和为 ,求证
,求证 .
.
已知函数 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求函数 的最小正周期和单调递增区间.
的最小正周期和单调递增区间.
如图,在四边形ABCD中,AB=8,BC=3,CD=5, ,
, .
.

(Ⅰ)求BD的长;
(Ⅱ)求 的面积.
的面积.
已知函数 .
.
(Ⅰ)若曲线 在点(0,1)处切线的斜率为-3,求函数
在点(0,1)处切线的斜率为-3,求函数 的单调区间;
的单调区间;
(Ⅱ)若函数 在区间[-2,
在区间[-2, ]上单调递增,求
]上单调递增,求 的取值范围.
的取值范围.
已知数列{ }的各项均不为0,其前
}的各项均不为0,其前 项和为Sn,且满足
项和为Sn,且满足 =
= ,
, =
= .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求{ }的通项公式;
}的通项公式;
(Ⅲ)若 ,求
,求 的最小值.
的最小值.
已知 为实数,用[
为实数,用[ ]表示不超过
]表示不超过 的最大整数,例如
的最大整数,例如 ,
, ,
, .对于函数
.对于函数 ,若存在
,若存在 且
且 ,使得
,使得 ,则称函数
,则称函数 是
是 函数.
函数.
(Ⅰ)判断函数 ,
, 是否是
是否是 函数;(只需写出结论)
函数;(只需写出结论)
(Ⅱ)已知 ,请写出
,请写出 的一个值,使得
的一个值,使得 为
为 函数,并给出证明;
函数,并给出证明;
(Ⅲ)设函数 是定义在
是定义在 上的周期函数,其最小周期为
上的周期函数,其最小周期为 .若
.若 不是
不是 函数,求
函数,求 的最小值.
的最小值.