命题:“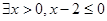 ”的否定是 .
”的否定是 .
椭圆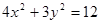 的焦距为 .
的焦距为 .
方程 表示圆,则
表示圆,则 的取值范围是 .
的取值范围是 .
已知命题 :
: ,命题
,命题 :
: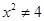 ,则
,则 是
是 的 条件.(选填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”)
的 条件.(选填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”)
若直线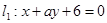 与
与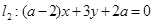 平行,则实数
平行,则实数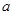 的值为 .
的值为 .
右焦点坐标是 ,且经过点
,且经过点 的椭圆的标准方程为 .
的椭圆的标准方程为 .
圆锥的体积为 ,底面积为
,底面积为 ,则该圆锥侧面展开图的圆心角大小为 .
,则该圆锥侧面展开图的圆心角大小为 .
过点 ,且在
,且在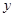 轴上的截距是在
轴上的截距是在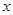 轴上的截距的
轴上的截距的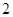 倍的直线方程是 .
倍的直线方程是 .
与圆 外切于原点,且半径为
外切于原点,且半径为 的圆的标准方程为 .
的圆的标准方程为 .
设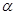 、
、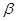 、
、 是三个不同的平面,
是三个不同的平面,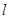 、
、 、
、 是三条不同的直线,则
是三条不同的直线,则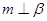 的一个充分条件为 .
的一个充分条件为 .
① ;
;
②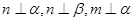 ;
;
③ ;
;
④ .
.
如图所示,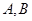 分别是椭圆的右、上顶点,
分别是椭圆的右、上顶点, 是
是 的三等分点(靠近点
的三等分点(靠近点 ),
), 为椭圆的右焦点,
为椭圆的右焦点, 的延长线交椭圆于点
的延长线交椭圆于点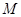 ,且
,且 ,则椭圆的离心率为 .
,则椭圆的离心率为 .

已知各顶点都在同一个球面上的正四棱锥高为 ,底面边长为
,底面边长为 ,则这个球的表面积是 .
,则这个球的表面积是 .
已知圆 和两点
和两点 ,若圆
,若圆 上不存在点
上不存在点 ,使得
,使得 为直角,则实数
为直角,则实数 的取值范围是 .
的取值范围是 .
已知圆
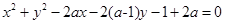
 对所有的
对所有的 且
且 总存在直线
总存在直线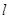 与圆
与圆 相切,则直线
相切,则直线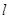 的方程为 .
的方程为 .
已知集合 ,
,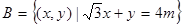 ,命题
,命题 :
: ,命题
,命题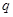 :方程
:方程 表示焦点在
表示焦点在 轴上的椭圆.
轴上的椭圆.
(1)若命题 为真命题,求实数
为真命题,求实数 的取值范围;
的取值范围;
(2)若“ ”为真,“
”为真,“ ”为假,求实数
”为假,求实数 的取值范围.
的取值范围.
如图,在三棱锥 中,平面
中,平面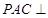 平面
平面 ,
,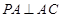 ,
, .设
.设 ,
,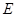 分别为
分别为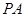 ,
, 中点.
中点.
(1)求证:
 平面
平面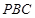 ;
;
(2)求证: 平面
平面 ;
;
(3)试问在线段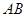 上是否存在点
上是否存在点 ,使得过三点
,使得过三点 ,
,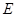 ,
, 的平面内的任一条直线都与平面
的平面内的任一条直线都与平面 平行?若存在,指出点
平行?若存在,指出点 的位置并证明;若不存在,请说明理由.
的位置并证明;若不存在,请说明理由.
已知 的顶点
的顶点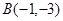 ,
, 边上的高
边上的高 所在直线的方程为
所在直线的方程为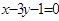 ,
, 边上中线
边上中线 所在直线的方程为
所在直线的方程为 .
.
求:(1)点 的坐标;
的坐标;
(2)直线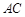 的方程.
的方程.
在平面直角坐标系 中,已知圆
中,已知圆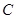 经过
经过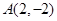 ,
,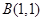 两点,且圆心在直线
两点,且圆心在直线 上.
上.
(1)求圆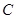 的标准方程;
的标准方程;
(2)过圆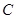 内一点
内一点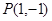 作两条相互垂直的弦
作两条相互垂直的弦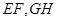 ,当
,当 时,求四边形
时,求四边形 的面积.
的面积.
(3)设直线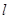 与圆
与圆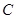 相交于
相交于 两点,
两点, ,且
,且 的面积为
的面积为 ,求直线
,求直线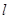 的方程.
的方程.
如图,在正方体 的棱长为
的棱长为 ,
, 为棱
为棱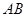 上的一动点.
上的一动点.

(1)若 为棱
为棱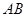 的中点,
的中点,
①求四棱锥 的体积
的体积
②求证:面 面
面
(2)若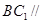 面
面 ,求证:
,求证: 为棱
为棱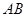 的中点.
的中点.
如图,在平面直角坐标系 中,椭圆
中,椭圆 过点
过点 ,离心率
,离心率 ,
, 为椭圆的左右焦点.
为椭圆的左右焦点.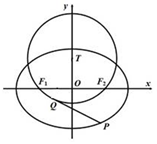
(1)求椭圆 的标准方程;
的标准方程;
(2)设圆 的圆心
的圆心 在
在 轴上方,且圆
轴上方,且圆 经过椭圆
经过椭圆 两焦点.点
两焦点.点 为椭圆
为椭圆 上的一动点,
上的一动点, 与圆
与圆 相切于点
相切于点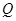 .
.
①当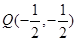 时,求直线
时,求直线 的方程;
的方程;
②当 取得最大值为
取得最大值为 时,求圆
时,求圆 方程.
方程.