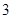 的相反数是( )
的相反数是( )
A.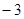 |
B.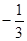 |
C.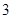 |
D.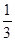 |
首届全国青运会于2015年10月18日在福州举行,据统计,共有28600名志愿者,将负责赛会服务、城市宣传、交通指引等工作,将这个数字用科学记数法表示为( ).
A.286×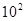 |
B.28.6×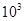 |
C.2.86× |
D.2.86×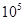 |
用四舍五入法,把2.345精确到0.01的近似数是( ).
| A.2.3 | B.2.34 | C.2.35 | D.2.30 |
若一个数的倒数等于这个数本身,则这个数是( )
| A.1 | B.-1 | C.1或-1 | D.0 |
下列各组运算中,结果为负数的是( )
A. |
B. |
C. |
D. |
一个矩形的周长为30,若矩形的一边长用字母 表示,则此矩形的面积为( )
表示,则此矩形的面积为( )
A. |
B. |
C. |
D. |
若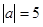 ,
,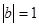 ,且
,且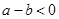 ,则
,则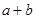 的值等于( )
的值等于( )
| A.4或6 | B.4或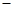 6 6 |
C.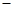 6或6 6或6 |
D.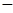 6或 6或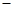 4 4 |
如果把汽车向东行驶8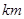 记作+8
记作+8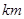 ,那么汽车向西行驶10
,那么汽车向西行驶10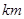 应记作
应记作 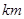 .
.
计算:|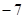 |= .
|= .
计算: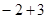 = .
= .
计算: 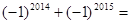 .
.
比较大小:
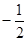 (选用“>”、“<”或“=”号填空).
(选用“>”、“<”或“=”号填空).
温度 ℃比
℃比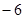 ℃高 ℃.
℃高 ℃.
“ 的2倍与
的2倍与 的
的 的和”用代数式表示为 .
的和”用代数式表示为 .
若 ,则
,则 =____________.
=____________.
已知数轴上有A、B两点,A点表示的数是 ,A、B两点的距离为3个单位长度,则满足条件的点B表示的数是 .
,A、B两点的距离为3个单位长度,则满足条件的点B表示的数是 .
如图所示,在直线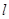 上有若干个点
上有若干个点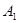 、
、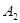 、…、
、…、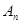 ,每相邻两点之间的距离都为1,点
,每相邻两点之间的距离都为1,点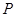 是线段
是线段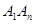 上的一个动点.
上的一个动点.
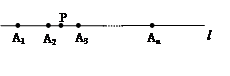
(1)当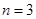 时,当点
时,当点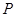 在点______(填
在点______(填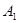 、
、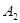 或
或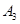 )的位置时,点
)的位置时,点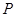 分别到点
分别到点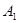 、
、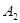 、
、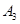 的距离之和最小;
的距离之和最小;
(2)当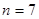 时,则点
时,则点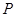 分别到点
分别到点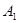 、
、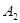 、…、
、…、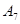 的距离之和的最小值是_________
的距离之和的最小值是_________
把下列各数分别填在相应的括号里:


 ,
, 
 ,
, 


整数集合{ … }
分数集合{ … }
负有理数集合{ … }
在所给的数轴上表示下列四个数,并把这四个数按从小到大的顺序,用“<”号连接起来.
-3, 0, - , 1
, 1

用“<”号连接起来: < < <
计算下列各题:
(1)
(2)
(3)
(4)
已知: 与
与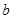 互为相反数,
互为相反数,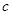 与
与 互为倒数,当
互为倒数,当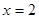 时,求代数式
时,求代数式 的值.
的值.
张亮用470元钱购买了8套儿童服装,准备以一定的价格出售.如果每套儿童服装以70元的价格作为标准价格来卖,超出为+,不足为-,那么8套儿童服装的销售记录如下(单位:元):
7 , -3 ,-1 ,-8 ,-2 ,+9 , 0 ,+6
当他卖完这8套服装盈利还是亏损,盈利或亏损多少元?
如图,长方形的长为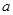 ,宽为
,宽为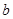 ,
,
(1)用含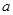 、
、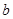 的代数式表示右图阴影部分的面积S阴影.
的代数式表示右图阴影部分的面积S阴影.
(2)当a=5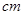 ,b=2
,b=2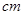 时,求S阴影.(
时,求S阴影.(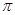 取3.14)
取3.14)
观察下列等式,探究其中的规律:
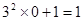
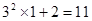
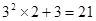
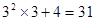
(1)根据以上观察,计算:① 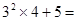
② 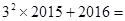
(2)猜想:当n为自然数时,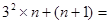
国庆放假时,小红一家三口一起乘小轿车去乡下探望爷爷、奶奶和外公、外婆.早上从家里出发,向东走了6千米到超市买东西,然后又向东走了1.5千米到爷爷家,中午从爷爷家出发向西走了12千米到外公家,晚上返回家里.
(1)若以家为原点,向东为正方向,用1个单位长度表示1千米,请将超市、爷爷家和外公家的位置在下面数轴上分别用点A、B、C表示出来;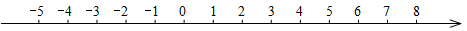
(2)问超市A和外公家C相距多少千米?
(3)若小轿车每千米耗油0.08升,求小红一家从出发到返回家所经历路程小车的耗油量.
某商场销售一种西装和领带,西装每套定价1000元,领带每条定价200元.“国庆节”
期间商场决定开展促销活动,活动期间向客户提供两种优惠方案.
方案一:买一套西装送一条领带;
方案二:西装和领带都按定价的90%付款.
现某客户要到该商场购买西装20套,领带x条(x>20).
(1)若该客户按方案一购买,需付款 元.(用含x的代数式表示)
若该客户按方案二购买,需付款 元.(用含x的代数式表示)
(2)若x=30,通过计算说明此时按(1)哪种方案购买较为合算?
(3)当x=30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法.