抛物线 的对称轴是( )
的对称轴是( )
A.直线 |
B.直线 |
C. 轴 轴 |
D.直线 |
已知(5,-1)是双曲线 上的一点,则下列各点中不在该图象上的是( )
上的一点,则下列各点中不在该图象上的是( )
A. |
B. |
C. |
D. |
已知 ,则下列各式中不正确的是( )
,则下列各式中不正确的是( )
A. |
B. |
C. |
D. |
在同一直角坐标系中,一次函数 和二次函数
和二次函数 的图象大致为 ( )
的图象大致为 ( )

若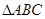 ∽
∽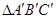 ,其面积比为
,其面积比为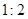 ,则
,则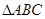 与
与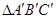 的相似比为( )
的相似比为( )
A.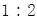 |
B.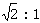 |
C. |
D.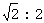 |
如图,在 中,
中, ,那么下列等式中,成立的是( )
,那么下列等式中,成立的是( )

A. |
B. |
C. |
D. |
已知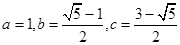 ,那么( )
,那么( )
| A.a是b 、c 的比例中项 |
| B.c是a、b的比例中项 |
| C.b是a、c的比例中项 |
| D.以上都不对 |
函数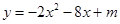 的图象上有两点
的图象上有两点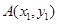 ,
,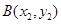 ,若
,若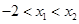 ,则( )
,则( )
A.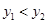 |
B.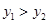 |
C. |
D.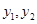 的大小不确定 的大小不确定 |
将抛物线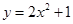 的图象向右平移2个单位,再向下平移3个单位,得到的抛物线是( )
的图象向右平移2个单位,再向下平移3个单位,得到的抛物线是( )
A.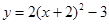 |
B.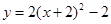 |
C.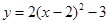 |
D.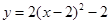 |
如图,在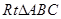 中,
中,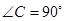 ,
,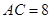 ,
,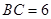 ,点
,点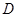 是
是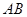 上的一个动点(不与
上的一个动点(不与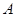 、
、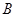 两点重合),
两点重合),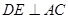 于点
于点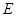 ,
,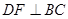 于点
于点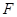 ,点
,点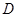 从靠近点
从靠近点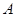 的某一点向点
的某一点向点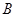 移动,矩形
移动,矩形 的周长变化情况是( )
的周长变化情况是( )
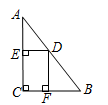
| A.逐渐减小 | B.逐渐增大 | C.先增大后减小 | D.先减小后增大 |
已知 、
、 是线段
是线段 的两个黄金分割点,且
的两个黄金分割点,且 ,则
,则 长为_________
长为_________
已知抛物线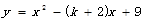 的顶点在
的顶点在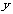 轴上,
轴上,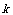 的值______________.
的值______________.
教练对小明推铅球的录像进行技术分析(如图),发现铅球行进高度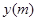 与水平距离
与水平距离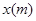 之间的关系为
之间的关系为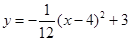 ,由此可知铅球推出的距离是____________
,由此可知铅球推出的距离是____________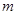 .
.
二次函数 的图象如图所示,以下结论:
的图象如图所示,以下结论:
① ;
;
② ;
;
③ ;
;
④ ;
;
⑤当 时,总有
时,总有
其中正确的有____________ (填写正确结论的序号)
如图,已知抛物线 的对称轴为直线
的对称轴为直线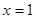 ,交
,交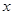 轴于
轴于 、
、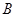 两点,交
两点,交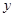 轴于
轴于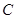 点,其中
点,其中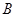 点的坐标为(3,0)。
点的坐标为(3,0)。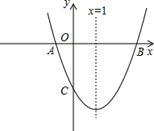
(1)直接写出 点的坐标;
点的坐标;
(2)求二次函数 的解析式。
的解析式。
如图是 的网格,正方形网格中的每个小正方形的边长都是,每个小正方形的顶点叫做格点,以格点为顶点的三角形叫格点三角形
的网格,正方形网格中的每个小正方形的边长都是,每个小正方形的顶点叫做格点,以格点为顶点的三角形叫格点三角形
(1)图1中的格点 与
与 相似吗?请说明理由.
相似吗?请说明理由.
(2)请在图2中画一个格点 与
与 相似(注意:
相似(注意: 与
与 、
、 都不全等)
都不全等)
已知函数 (
(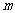 为常数).
为常数).
(1)证明:无论m取何值,该函数与 轴总有两个交点;
轴总有两个交点;
(2)设函数的两交点的横坐标分别为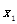 和
和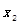 ,且
,且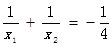 ,求此函数的解析式.
,求此函数的解析式.
如图,一次函数 与反比例函数
与反比例函数 的图象交于
的图象交于 、
、 两点.
两点.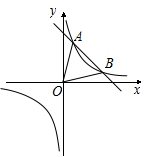
(1)求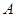 、
、 两点的坐标和反比例函数的解析式;
两点的坐标和反比例函数的解析式;
(2)根据图象,直接写出当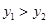 时
时 的取值范围;
的取值范围;
(3)求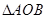 的面积.
的面积.
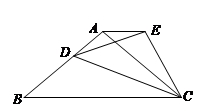
如图,在等腰三角形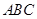 中,
中, ,
,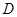 是
是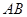 边上一点,以
边上一点,以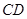 为一边,向上作等腰
为一边,向上作等腰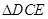 ,使
,使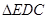 ∽
∽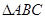 ,连
,连 ,
,
求证:(1)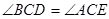 (2)
(2)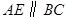
为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为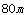 的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设
的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设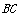 的长度为
的长度为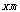 ,矩形区域
,矩形区域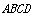 的面积为
的面积为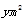 .
.
(1)求y与x之间的函数关系式,并注明自变量x的取值范围;
(2)x为何值时,y有最大值?最大值是多少?