9的算术平方根是( )
A. |
B. |
C.3 | D. |
计算 的结果是( )
的结果是( )
A. |
B. |
C.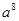 |
D.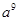 |
下列式子中,属于最简二次根式的是( )
A. |
B. |
C. |
D. |
在 ,
, ,
, ,
, 这四个数中,是无理数的是( )
这四个数中,是无理数的是( )
A. |
B. |
C. |
D. |
下列说法错误的是( )
| A.9的算术平方根是3 |
B.16的平方根是 |
C.27的立方根是 |
D.立方根等于 的实数是 的实数是 |
下列计算正确的是( )
A. |
B. |
C. |
D. |
已知 、
、 是两个连续的整数,且
是两个连续的整数,且 ,
, 则等于( )
则等于( )
| A.7 | B.8 | C.9 | D.10 |
下列各式变形中,是因式分解的是( )
A.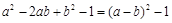 |
B. |
C.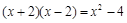 |
D.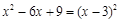 |
下列二次根式中,与 是同类二次根式的是( )
是同类二次根式的是( )
A. |
B. |
C. |
D. |
若 ,则
,则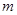 的值是( )
的值是( )
| A.1 | B.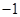 |
C.9 | D.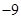 |
若  ,
, ,则
,则 、
、 的关系为( )
的关系为( )
A. |
B. 、 、 互为倒数 互为倒数 |
C. |
D. 、 、 互为相反数 互为相反数 |
若 ,
, ,则
,则 的值是( )
的值是( )
A. |
B. |
C. |
D. |
 的相反数是 .
的相反数是 .
计算: = .
= .
计算: = .
= .
若多项式 是一个完全平方式,则实数
是一个完全平方式,则实数 的值为 .
的值为 .
如图,在长方形花园 中,
中, ,
, ,花园中建有一条长方形道路
,花园中建有一条长方形道路 及一条平行四边形道路
及一条平行四边形道路 .若
.若 ,其中
,其中 .则花园中可绿化部分的面积为 .
.则花园中可绿化部分的面积为 .

如图,在 中,
中, ,
, ,
, ,若四边形
,若四边形 的面积为
的面积为 ,则
,则 的面积为 .
的面积为 .

计算: .
.
计算: .
.
(1)解方程:
(2)分解因式:
计算: .
.
先化简,再求值: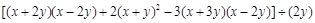 ,其中
,其中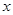 ,
,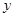 满足
满足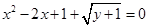 .
.
图①是一个长为 、宽为
、宽为 的长方形,用这样四个全等的长方形,拼成如图②的正方形.
的长方形,用这样四个全等的长方形,拼成如图②的正方形.

(1)按要求填空:
ⅰ.请用含字母 、
、 的代数式表示图②中的阴影部分的正方形的边长: ;
的代数式表示图②中的阴影部分的正方形的边长: ;
ⅱ.请用含字母 、
、 的代数式,用两种不同的方法表示图②中阴影部分的面积:
的代数式,用两种不同的方法表示图②中阴影部分的面积:
方法1:
方法2:
ⅲ.观察图②,请写出代数式 、
、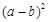 、
、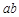 之间的等量关系: ;
之间的等量关系: ;
(2)根据(1)题中的等量关系,解决如下问题:
若 ,
, ,求
,求 的值.
的值.
阅读以下材料:
对于实数 、
、 、
、 定义两种新运算,规定
定义两种新运算,规定 表示这三个数的平均数,
表示这三个数的平均数, 表示这三个数中最小的数,例如:
表示这三个数中最小的数,例如: ;
; .
.
(1)求 的值;
的值;
(2)已知 对于任意实数
对于任意实数 、
、 、
、 都成立,则
都成立,则 、
、 、
、 应满足怎样的关系式?
应满足怎样的关系式?
(3)已知 ,求
,求 的值.
的值.
如图,利用一面墙(墙的长度为20米),用36米长的篱笆围成两个长方形鸡场,鸡场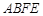 与鸡场
与鸡场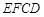 ,中间
,中间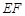 用一道篱笆隔开,每个鸡场均留一道1米宽的门,设
用一道篱笆隔开,每个鸡场均留一道1米宽的门,设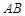 的长为
的长为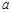
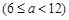 米.
米.
(1)当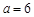 时,求点
时,求点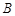 到点
到点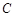 的距离;
的距离;
(2)用含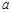 的代数式表示两个鸡场的面积和,并将所得式子化简;
的代数式表示两个鸡场的面积和,并将所得式子化简;
(3)两个鸡场的面积和有最大值吗?若有,请求出最大值;若没有,请说明理由.