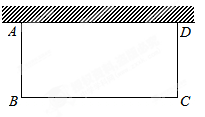
4的平方根是（ ）
| A．±2 | B．2 | C．-2 | D．±4 |
下列实数中，是无理数的为（ ）
| A．－3 | B． |
C．－ |
D．0 |
下列运算中，计算结果正确的是（ ）
A． |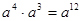
B． |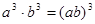
C． |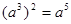
D． |
下列命题中是真命题的是（ ）
A． 是无理数 |
| B．相等的角是对顶角 |
C． |
| D．-27没有立方根 |
下列运算正确的是 （ ）
A． |
B． |
C． |
D． |
下列因式分解错误的是（ ）
A． |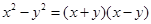
B． |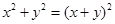
C． |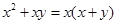
D． |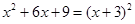
一个正方形的边长为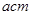
，若它的边长增加
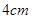,则面积增加了（ ）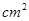
| A．16 | B．8 |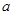
C．（16+4） |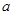
D．（16+8） |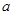
64的立方根为 ．
计算：
= ．
把命题“同旁内角互补，两直线平行”改写成“如果……，那么……”的形式：______．
比较大小：2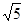 
因式分解：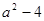
= ．
若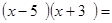
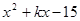，则
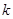的值为 ．
已知
，则化简：
．
已知多项式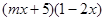
展开后不含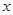
的一次项，则
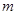的值是 ．
当整数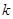
= 时，多项式
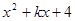恰好是另一个完全平方式．
我们把分子为1的分数叫做理想分数，如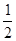
，
，
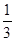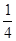，…，任何一个理想分数都可以写成两个不同理想分数的和，如
；
；
；
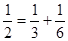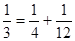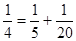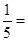；﹍根据对上述式子的观察，请你思考：如果理想分数
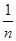（n是不小于2的整数）
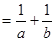，那么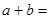
．（用含n的式子表示）．
计算：
计算： 
因式分解：
先化简，再求值: 
，其中
= 
若
，
．求：
（1）
的值；
（2）
的值．
若
与
的积与
是同类项，求
的平方根
如图，有一块长为
，宽为
的长方形铁皮，将其四个角分别剪去一个边长为
（
>1）的正方形，剩余的部分可制成一个无盖的长方体盒子。（损失的忽略不计）则长方体盒子的底面的长AB= ，AD= ．求这个盒子的容积
图1是一个长为2
，宽为2
的长方形，沿图中虚线剪开，可分成四块小长方形．
（1）求出图1的长方形面积；
（2）将四块小长方形拼成一个图2的正方形．利用阴影部分面积的不同表示方法，直接写出代数式（
）2、（
）2、
之间的等量关系；
（3）把四块小长方形不重叠地放在一个长方形的内部（如图3），未被覆盖的部分用阴影表示．求两块阴影部分的周长和（用含
、
的代数式表示）．
先阅读理解下面的例题，再按要求解答下列问题：
例题 ：求代数式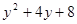
的最小值．
解：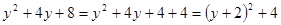 
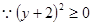
的最小值是
．
（1）代数式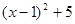
的最小值 ；
（2）求代数式
的最小值；
（3）某居民小区要在一块一边靠墙（墙长
）的空地上建一个长方形花园
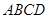，花园一边靠墙，另三边用总长为
的栅栏围成．如图，设
（），请问:当
取何值时，花园的面积最大？最大面积是多少？
