函数 的定义域是( )
的定义域是( )
A. |
B. |
C. |
D. |
已知复数 在复平面上对应的点位于第二象限,且
在复平面上对应的点位于第二象限,且 (其中
(其中 是虚数单位),则实数
是虚数单位),则实数 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
函数 在
在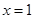 处的切线方程是( )
处的切线方程是( )
A.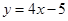 |
B. |
C. |
D. |
等差数列 的前n项和为
的前n项和为 ,已知
,已知 ,
, ,则
,则 ( )
( )
| A.1 | B.2 | C.3 | D.4 |
已知: 表示不同的直线,
表示不同的直线, 表示不同的平面,现有下列命题:①
表示不同的平面,现有下列命题:① ,②
,② ,③
,③ ,④
,④ ,其中真命题有( )
,其中真命题有( )
| A.0个 | B.1个 | C.2个 | D.3个 |
在 中,
中, 为中线
为中线 上一个动点,若
上一个动点,若 ,则
,则 的最小值是( )
的最小值是( )
| A.2 | B.-1 | C.-2 | D.-4 |
如图,正方体 中,
中, 棱
棱 的中点,用过点
的中点,用过点 的平面截去该正方体的上半部分,则剩余几何体的左视图为( )
的平面截去该正方体的上半部分,则剩余几何体的左视图为( )

A. |
B. |
C. |
D. |
已知函数 的图象上相邻两个最高点的距离为
的图象上相邻两个最高点的距离为 .若将函数
.若将函数 的图象向左平移
的图象向左平移 个单位长度后,所得图象关于
个单位长度后,所得图象关于 轴对称,则
轴对称,则 的解析式为( )
的解析式为( )
A. |
B. |
C. |
D. |
运行如图所示的流程图,则输出的结果 是( )
是( )

A. |
B. |
C. |
D. |
已知 ,则函数
,则函数 为增函数的概率为( )
为增函数的概率为( )
A. |
B. |
C. |
D. |
已知 ,
, 满足约束条件
满足约束条件 ,若
,若 的最大值为
的最大值为 ,则
,则 ( )
( )
A. |
B. |
C.1 | D.2 |
已知直线 经过抛物线
经过抛物线 的焦点,与
的焦点,与 交于
交于 两点,若
两点,若 ,则
,则 的值为( )
的值为( )
A. |
B. |
C.1 | D.2 |
“ ”是“直线
”是“直线 与直线
与直线 垂直”的________条件.
垂直”的________条件.
设 的内角
的内角 的对边分别为
的对边分别为 ,且
,且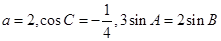 ,则
,则 ________.
________.
函数 是定义在
是定义在 上的奇函数,并且当
上的奇函数,并且当 时,
时, ,那么
,那么 ________.
________.
在平面直角坐标系 中,以点
中,以点 为圆心,且与直线
为圆心,且与直线 相切的所有圆中,半径最大的圆的标准方程是________.
相切的所有圆中,半径最大的圆的标准方程是________.
在数列 中,
中, ,数列
,数列 是首项为9,公比为3的等比数列.
是首项为9,公比为3的等比数列.
(Ⅰ)求 的值;
的值;
(Ⅱ)求数列 的前n项和
的前n项和 .
.
某校高三年级学生600名,从参加期中考试的学生中随机抽出某班学生(该班共50名同学),并统计了他们的数学成绩(成绩均为整数且满分为150分),数学成绩分组及各组频数如下表:
| 分组 |
频数 |
频率 |
 |
2 |
0.04 |
 |
4 |
0.08 |
 |
8 |
0.16 |
 |
11 |
0.22 |
 |
15 |
0.30 |
 |
 |
 |
 |
4 |
0.08 |
| 合计 |
50 |
1 |
(1)写出 的值;
的值;
(2)估计该校高三学生数学成绩在120分以上学生人数;
(3)该班为提高整体数学成绩,决定成立“二帮一”小组,即从成绩在 中选两位同学,来帮助成绩在
中选两位同学,来帮助成绩在 中的某一位同学,已知甲同学的成绩为56分,乙同学的成绩为145分,求甲乙在同一小组的概率.
中的某一位同学,已知甲同学的成绩为56分,乙同学的成绩为145分,求甲乙在同一小组的概率.
如图,已知四棱锥 ,
,  ,
,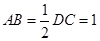 ,
,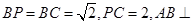 平面
平面 ,
,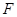 为
为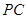 中点.
中点.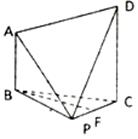
(Ⅰ)求证: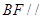 平面
平面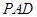 ;
;
(Ⅱ)求证:平面 平面
平面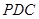 .
.
已知椭圆 过点
过点 ,且离心率
,且离心率 .
.
(Ⅰ)求椭圆方程;
(Ⅱ)若直线 与椭圆交于不同的两点
与椭圆交于不同的两点 ,且线段
,且线段 的垂直平分线过定点
的垂直平分线过定点 ,求
,求 的取值范围.
的取值范围.
已知函数 ,
,
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)若函数 在在区间
在在区间 上的最小值为0,求
上的最小值为0,求 的值.
的值.
如图, 是圆
是圆 的直径,直线
的直径,直线 与圆
与圆 相切于
相切于 ,
, 垂直
垂直 于
于 ,
, 垂直
垂直 于
于 ,
, 垂直
垂直 于
于 ,
, 垂直
垂直 于
于 ,连接
,连接 ,证明:
,证明:
(Ⅰ) ;
;
(Ⅱ) .
.
在直角坐标系 中,以
中,以 为极点,
为极点, 轴正半轴为极轴建立极坐标系.圆
轴正半轴为极轴建立极坐标系.圆 ,直线
,直线 的极坐标方程分别为
的极坐标方程分别为 .
.
(Ⅰ)求 与
与 交点的极坐标;
交点的极坐标;
(Ⅱ)设 为
为 的圆心,
的圆心, 为
为 与
与 交点连线的中点.已知直线
交点连线的中点.已知直线 的参数方程为
的参数方程为 (
( 为参数),求
为参数),求 的值.
的值.
已知函数 ,其中
,其中 .
.
(Ⅰ)当 时,求不等式
时,求不等式 的解集;
的解集;
(Ⅱ)已知关于x的不等式 的解集为
的解集为 ,求
,求 的值 .
的值 .