设全集
，集合
，则集合
．
已知集合
,则集合
的子集共有 个．
函数
定义域为 ．
若函数
为奇函数，则实数
的值为 ．
设集合
，若
，则
的值为 ．
已知函数
，则
．
已知三个数
，则
的大小关系为 ．（用“<”连接）
如果指数函数
在
上的最大值与最小值的和为
，则实数
．
已知函数
在
上为减函数，则
的取值范围是 ．
若函数
的零点在区间
内
,则
．
已知函数
，若
，则
= ．
设定义在
上的函数
同时满足以下三个条件：①
；②
；③当
时，
，则
．
已知函数
，若对任意实数b，总存在实数
，使得
成立，则实数a的取值范围是 ．
已知
或
;
（1）若
，求实数
的取值范围；
（2）若
，求实数的取值范围．
（1）求值：
；
（2）已知
，求
的值．
已知函数
，
，且
．
（1）求实数
的值；
（2）作出函数
的图象并直接写出单调减区间．
为治疗一种慢性病，某医药研究所研究出一种新型药物，病人按规定的剂量服用该药物后，测得每毫升血液中含药量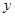
（毫克）与时间
（小时）满足：前1小时内成正比例递增，1小时后按指数型函数
（
为常数）衰减．如图是病人按规定的剂量服用该药物后，每毫升血液中药物含量随时间变化的曲线．
（1）求函数
的解析式；
（2）已知每毫升血液中含药量不低于0．5毫克时有治疗效果，低于0．5毫克时无治疗效果．求病人一次服药后的有效治疗时间为多少小时？
已知函数
的定义域为
．
（1）判断函数
的单调性，并用定义给出证明；
（2）若实数
满足
，求的取值范围．
已知函数
．
（1）证明
为偶函数；
（2）若不等式
在
上恒成立，求实数
的取值范围；
（3）当x∈
（m>0，n>0）时，函数
的值域为[2－3m,2－3n]，求实数t的取值范围．