已知全集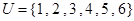 ,
,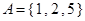 ,
,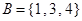 ,则
,则 ( ).
( ).
A.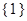 |
B.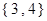 |
C. |
D.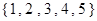 |
下列式子中,正确的是( )
A.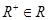 |
B.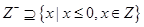 |
| C.空集是任何集合的真子集 |
D. |
若集合 ,
,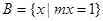 ,且
,且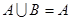 ,则
,则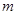 的值为( )
的值为( )
A.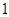 |
B. |
C.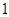 或 或 |
D.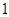 或 或 或 或 |
设I为全集,集合M,N,P都是其子集,则图中的阴影部分表示的集合为( ).
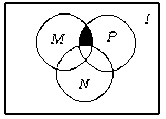
| A.M∩(N∪P) | B.M∩(P∩ IN) IN) |
C.P∩( IN∩ IN∩ IM ) IM ) |
D.(M∩N)∪(M∩P) |
已知函数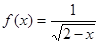 的定义域为
的定义域为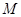 ,
,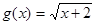 的定义域为
的定义域为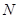 ,则
,则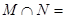 ( )
( )
A.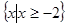 |
B.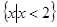 |
C.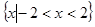 |
D. |
下列各组表示同一函数的是( )
A.  与 与 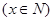 |
B.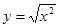 与 与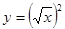 |
C. |
D. 与 与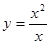 |
下列四个函数中,在(0,∞)上为增函数的是( )
A.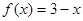 |
B.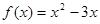 |
C.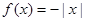 |
D.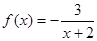 |
已知函数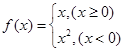 ,则
,则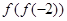 的值是( )
的值是( )
| A.2 | B.4 | C. |
D. |
函数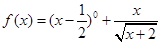 的定义域为( )
的定义域为( )
A.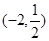 |
B.(-2,+∞) | C.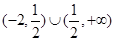 |
D.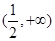 |
函数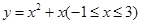 的值域是 ( )
的值域是 ( )
A.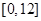 |
B.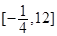 |
C.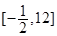 |
D.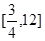 |
已知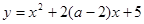 在区间
在区间 上是增函数,则
上是增函数,则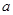 的范围是( )
的范围是( )
A.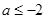 |
B.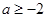 |
C.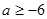 |
D.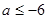 |
设函数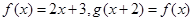 ,则
,则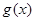 的表达式是( )
的表达式是( )
A. |
B.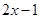 |
C.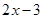 |
D.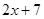 |
设集合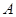 、
、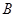 都是
都是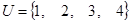 的子集,已知(
的子集,已知(
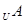 )
)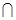 (
(
 )
)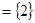 ,(
,(
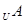 )
)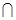
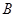
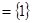 ,则
,则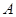 等于 .
等于 .
已知函数 在区间[0,1]上的值恒正,则实数
在区间[0,1]上的值恒正,则实数 的取值范围是 .
的取值范围是 .
已知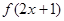 定义域为
定义域为 ,则
,则 定义域为 ;
定义域为 ;
已知 ,
, ,且A∩B=B,则
,且A∩B=B,则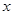 的值为___________.
的值为___________.
已知集合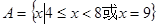 ,
,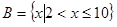 ,
,
(1)求 ,
,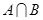 ;
;
(2) ,
,
设全集为R,已知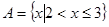 ,
,
(1)若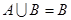 ,求实数
,求实数 的取值范围
的取值范围
(2)若 ,求实数
,求实数 的取值范围
的取值范围
(3)若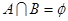 ,求实数
,求实数 的取值范围
的取值范围
已知函数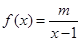 ,
, .
.
(1)若点(4, )在函数
)在函数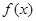 的图像上,求
的图像上,求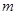 的值;
的值;
(2)若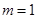 ,判断函数
,判断函数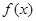 的单调性,并证明;
的单调性,并证明;
(3)若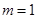 ,求
,求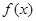 的值域.
的值域.
如图,已知底角为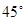 的等腰梯形
的等腰梯形 ,底边
,底边 长为7
长为7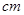 ,腰长为
,腰长为 ,当一条垂直于底边
,当一条垂直于底边 垂足为
垂足为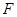 的直线
的直线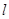 由
由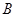 从左至右向
从左至右向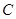 移动(与梯形
移动(与梯形 有公共点)时,直线
有公共点)时,直线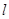 把梯形分成两部分,令
把梯形分成两部分,令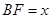
 ,记左边部分的面积为
,记左边部分的面积为 .
.
(1)试求 1,
1, 3时的
3时的 值;
值;
(2)写出 关于
关于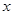 的函数关系式.
的函数关系式.
若 是定义在(0, +∞)上的增函数,且对一切
是定义在(0, +∞)上的增函数,且对一切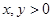 ,都满足
,都满足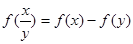 ,
,
(1)求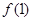 的值;
的值;
(2)若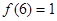 ,解不等式
,解不等式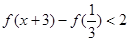 .
.
已知二次函数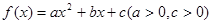 的图像与
的图像与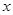 轴有两个不同的公共点,且有
轴有两个不同的公共点,且有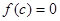 ,当
,当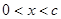 时,恒有
时,恒有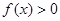 、
、
(1)试比较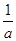 与c的大小;
与c的大小;
(2)试求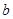 的取值范围;
的取值范围;
(3)若以二次函数的图像与坐标轴的三个交点为顶点的三角形的面积为5,求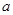 的取值范围
的取值范围