数列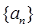 为等差数列,
为等差数列,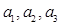 为等比数列,
为等比数列,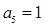 ,则
,则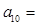 ( )
( )
A.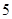 |
B.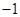 |
C. |
D.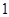 |
给出如下四个命题:
①若“p且q”为假命题,则p、q均为假命题;
②命题“若a>b,则2a>2b﹣1”的否命题为“若a ≤ b,则2a ≤ 2b﹣1”;
③“ x∈R,
x∈R,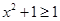 ”的否定是“
”的否定是“ x∈R,
x∈R,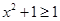 ;
;
④在△ABC中,“A>B”是“sinA>sinB”的充要条件.
其中不正确的命题的个数是( )
| A.4 | B.3 | C.2 | D.1 |
已知命题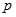 :“
:“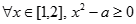 ”,命题
”,命题 :“
:“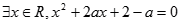 ”.若命题“
”.若命题“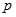 且
且 ”是真命题,则实数
”是真命题,则实数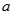 的取值范围为( )
的取值范围为( )
A.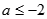 或 或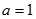 |
B.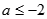 或 或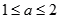 |
C. |
D. |
若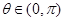 ,且
,且 ,则曲线
,则曲线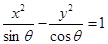 是( )
是( )
A.焦点在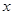 轴上的椭圆 轴上的椭圆 |
B.焦点在 轴上的椭圆 轴上的椭圆 |
C.焦点在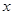 轴上的双曲线 轴上的双曲线 |
D.焦点在 轴上的双曲线 轴上的双曲线 |
已知点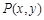 在不等式组
在不等式组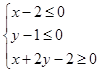 表示的平面区域内运动,则
表示的平面区域内运动,则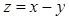 的最大值是( )
的最大值是( )
A.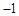 |
B.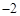 |
C.2 | D.3 |
在公差不为0的等差数列 中,
中,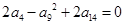 ,数列
,数列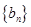 是等比数列,且
是等比数列,且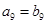 ,则
,则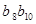 =( )
=( )
| A.4 | B.16 | C.8 | D.2 |
已知向量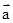 =(2,4,5),
=(2,4,5),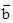 =(3,x,y),
=(3,x,y),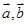 分别是直线
分别是直线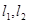 的方向向量,若
的方向向量,若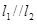 ,则( )
,则( )
| A.x=6、y=15 | B.x=3、y=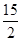 |
| C.x=3、y=15 | D.x=6、y=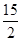 |
在△ABC中,内角A,B,C所对的边分别是a,b,c.若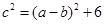 ,C=
,C=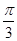 ,则△ABC
,则△ABC
的面积是( )
| A.3 | B.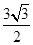 |
C.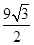 |
D.3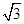 |
若直线mx+ny+2=0(m>0,n>0)截得圆 的弦长为2,则
的弦长为2,则 的最小值为( )
的最小值为( )
| A.4 | B.12 | C.16 | D.6 |
已知F是抛物线 的焦点,A,B为抛物线上的两点,且|AF|+|BF|=3,则线段AB的中点M到y轴的距离为( )
的焦点,A,B为抛物线上的两点,且|AF|+|BF|=3,则线段AB的中点M到y轴的距离为( )
A. |
B. |
C. |
D. |
已知直线 与椭圆
与椭圆 相交于A、B两点,若椭圆的离心率为
相交于A、B两点,若椭圆的离心率为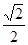 ,焦距为2,则线段AB的长是( )
,焦距为2,则线段AB的长是( )
A. B.
B.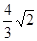 C.
C. D.
D.
设双曲线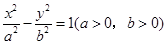 的右焦点为
的右焦点为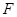 ,过点
,过点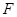 作与
作与 轴垂直的直线
轴垂直的直线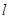 交两渐近线于
交两渐近线于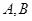 两点,且与双曲线在第一象限的交点为
两点,且与双曲线在第一象限的交点为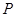 ,设
,设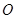 为坐标原点,若
为坐标原点,若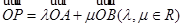 ,
,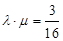 ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A.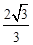 |
B.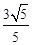 |
C. |
D.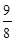 |
抛物线 的准线方程为 .
的准线方程为 .
已知等比数列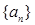 的前
的前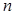 项和为
项和为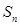 ,若
,若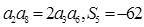 ,则
,则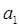 的值是 .
的值是 .
若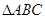 的面积为
的面积为 ,则角
,则角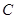 =__________.
=__________.
已知动圆M与圆C1:(x+5)2+y2=16外切,与圆C2:(x-5)2+y2=16内切,则动圆圆心的轨迹方程为 .
已知命题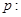 “存在
“存在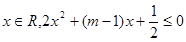 ”,命题
”,命题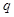 :“曲线
:“曲线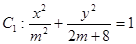 表示焦点在
表示焦点在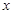 轴上的椭圆”,命题
轴上的椭圆”,命题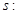 “曲线
“曲线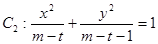 表示双曲线”.
表示双曲线”.
(1)若“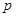 且
且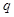 ”是真命题,求
”是真命题,求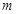 的取值范围;
的取值范围;
(2)若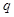 是
是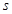 的必要不充分条件,求
的必要不充分条件,求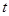 的取值范围.
的取值范围.
在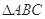 中,内角
中,内角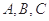 所对边分别为
所对边分别为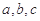 ,且
,且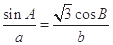 .
.
(1)求角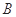 的大小;
的大小;
(2)如果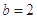 ,求
,求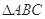 面积的最大值.
面积的最大值.
在等比数列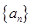 中,
中,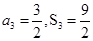 .
.
(Ⅰ)求数列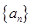 的通项公式;
的通项公式;
(Ⅱ)设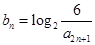 ,且
,且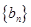 为递增数列,若
为递增数列,若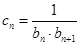 ,求证:
,求证: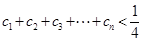 .
.
设函数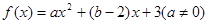 .
.
(1)若不等式 的解集
的解集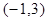 ,求
,求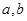 的值;
的值;
(2)若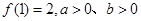 ,求
,求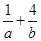 的最小值.
的最小值.
如图,四边形 是正方形,△
是正方形,△ 与△
与△ 均是以
均是以 为直角顶点的等腰直角三角形,点
为直角顶点的等腰直角三角形,点 是
是 的中点,点
的中点,点 是边
是边 上的任意一点.
上的任意一点.
(1)求证: ;
;
(2)求二面角 的平面角的正弦值.
的平面角的正弦值.
已知椭圆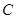 :
: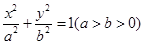 的离心率为
的离心率为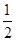 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线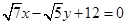 相切.
相切.
(1)求椭圆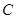 的方程;
的方程;
(2)设 ,过点
,过点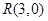 作与
作与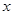 轴不重合的直线
轴不重合的直线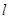 交椭圆
交椭圆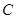 于
于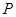 ,
, 两点,连接
两点,连接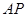 ,
,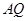 分别交直线
分别交直线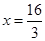 于
于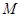 ,
,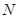 两点,若直线
两点,若直线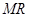 、
、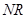 的斜率分别为
的斜率分别为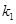 、
、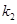 ,试问:
,试问: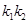 是否为定值?若是,求出该定值,若不是,请说明理由.
是否为定值?若是,求出该定值,若不是,请说明理由.