函数 的定义域为( )
的定义域为( )
A. |
B. |
C. |
D. |
三个数 之间的大小关系是( )
之间的大小关系是( )
A. |
B. |
C. |
D. |
下面各组函数中为相同函数的是( )
A. |
B. |
C. |
D. |
已知函数 在
在 上为奇函数,且当
上为奇函数,且当 时,
时, ,则当
,则当 时,
时, 的解析式是( )
的解析式是( )
A. |
B. |
C. |
D. |
已知函数 ,
, ,
, (其中
(其中 且
且 ),在同一坐标系中画出其中两个函数在第一象限内的大致图像,其中正确的是( )
),在同一坐标系中画出其中两个函数在第一象限内的大致图像,其中正确的是( )




设 为全集,集合
为全集,集合 是集合
是集合 的子集,且满足条件
的子集,且满足条件 ,那么下列各式中一定成立的是( )
,那么下列各式中一定成立的是( )
A. |
B. |
C. |
D. |
已知实数 满足不等式
满足不等式 则不可能成立的是( )
则不可能成立的是( )
A. |
B. |
C. |
D. |
设函数 ,若
,若 ,则满足条件的所有实数
,则满足条件的所有实数 的取值范围为( )
的取值范围为( )
A. |
B. |
C. |
D. |
设全集 ,
, ,
, ,则
,则 __________ ,
__________ , ______________.
______________.
设函数 , 则
, 则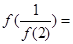 ,若
,若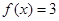 ,则
,则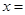 .
.
若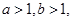 且
且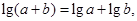 则
则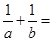 ,
,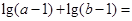 .
.
函数 的单调递减区间是____________,值域为____________.
的单调递减区间是____________,值域为____________.
满足条件 的集合
的集合 有 个.
有 个.
用 表示两数中的最小值,若函数
表示两数中的最小值,若函数 ,则不等式
,则不等式 的解集是________________________.
的解集是________________________.
当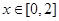 时,函数
时,函数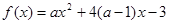 在
在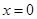 时取得最大值,则
时取得最大值,则 的取值范围是________________________.
的取值范围是________________________.
已知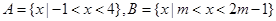 .
.
(1)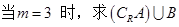 ;
;
(2)若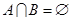 ,求实数
,求实数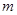 的取值范围.
的取值范围.
有甲、乙两种商品,经营销售这两种商品所能获得的利润依次是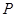 (万元)和
(万元)和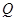 (万元),它们与投入资金
(万元),它们与投入资金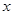 (万元)的关系有经验公式:
(万元)的关系有经验公式: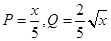 .今有
.今有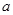 万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少?能获得最大利润是多少?
万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少?能获得最大利润是多少?
(1)已知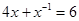 ,求
,求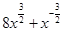 的值;
的值;
(2)若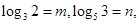 用
用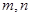 表示
表示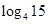 .
.
设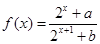 是定义在
是定义在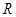 上的奇函数(
上的奇函数( 为实常数).
为实常数).
(1)求 与
与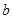 的值;
的值;
(2)证明函数 的单调性并求函数
的单调性并求函数 的值域.
的值域.
已知函数 ,其中
,其中 .
.
(1)当 ,求函数
,求函数 的单调区间;
的单调区间;
(2)若不等式 在
在 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.