设集合
（ ）
A． |
B． |
C． |
D． |
命题“∀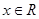
，
|
|
”的否定是（ ）
A．∀， || |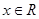
B．∀， || |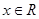
C．∃ ，| | |
D．∃，|| |
已知平面向量
，且
，则
（ ）
A． |
B． |
C． |
D． |
函数
的定义域为（ ）
A． |
B． |
C． |
D． |
△ABC中，BC＝2，B＝
，当△ABC的面积等于
时，sin C的值为（ ）
| A． |
B． |
C． |
D． |
使命题“对任意的x∈[1,2],
”为真命题的一个充分不必要条件是（ ）
A． ≥4 |
B．≤4 |
C．≥5 |
D．a≤5 |
在△ABC中，角A，B，C所对的边分别是a，b，c，若acos B＝bcos A，则△ABC是（ ）
| A．等腰三角形 | B．直角三角形 |
| C．等腰直角三角形 | D．等腰或直角三角形 |
下边程序框图中，若输入
，
，则输出
的值别是（ ）
A． |
B． |
C． |
D． |
一个几何体的三视图如图所示，则该几何体的体积为（ ）
A． |
B． |
C． |
D． |
设偶函数
对任意
都有
，且当
时，
，则
（ ）
| A．10 | B． |
C． |
D． |
已知三棱锥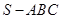
的底面是以
为斜边的等腰直角三角形,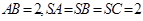
，则三棱锥的外接球的球心到平面
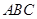的距离是（ ）
A． |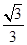
B．1 | C． |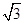
D． |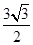
直线
过抛物线
的焦点，且交抛物线于
两点，交其准线于
点,已知
,则
（ ）
| A．2 | B． |
C． |
D．4 |
若变量
满足约束条件：
，则
的最大值为 ．
设
是实数，若复数
（为虚数单位）在复平面内对应的点在直线
上，则的值为 ．
若函数
对任意的
恒成立，则
．
我们把离心率
的双曲线
称为黄金双曲线．如图是双曲线
的图象，给出以下几个说法：
①双曲线
是黄金双曲线；
②若
，则该双曲线是黄金双曲线；
③若
为左右焦点，
为左右顶点，
且
，则该双曲线是黄金双曲线；
④若
经过右焦点
且
，
，则该双曲线是黄金双曲线．
其中正确命题的序号为 ．
已知
是等差数列，满足
，数列
满足
，且
为等比数列．
（1）求数列
的通项公式；
（2）求数列的前n项和．
某班50名学生在一次百米测试中，成绩全部介于13秒与18秒之间，将测试结果按如下方式分成五组：第一组
，第二组
，
，第五组
.下图是按上述分组方法得到的频率分布直方图.按上述分组方法得到的频率分布直方图.
（Ⅰ）若成绩大于或等于14秒且小于16秒认为良好，求该班在这次百米测试中成绩良好的人数；
（Ⅱ）设m,n表示该班某两位同学的百米测试成绩，且已知
求事件“
”发生的概率.
如图，在四棱锥
中，
，
平面
，
平面，
，
，
．
（Ⅰ）求棱锥
的体积；
（Ⅱ）求证：平面
平面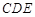
；
（Ⅲ）在线段
上是否存在一点
，使
平面
？若存在，求出
的值；若不存在，说明理由．
已知椭圆
的左顶点为
，
是椭圆
上异于点的任意一点，点
与点关于点对称．
（1）若点的坐标为
，求
的值；
（2）若椭圆上存在点，使得
，求的取值范围．
已知函数
R）.
（1）若曲线
在点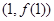
处的切线与直线
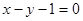平行，求
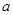的值；
（2）在（1）条件下，求函数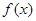
的单调区间和极值；
（3）当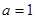
，且
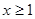时，证明：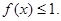
选修4－1：几何证明选讲．
如图，在
中，
是
的角平分线，
的外接圆交
于点
，
．
（Ⅰ）求证：
；
（Ⅱ）当
时，求
的长．
选修4-4：坐标系与参数方程选讲
在直角坐标系
中，曲线
的参数方程为
（
为参数），以原点为极点，以
轴正半轴为极轴，建立极坐标系，曲线
的极坐标方程为
．
（1）求曲线的普通方程与曲线的直角坐标方程；
（2）设点
，曲线与曲线交于
，求
的值．
选修4-5：不等式选讲
已知函数
．
（1）证明：
；
（2）求不等式
的解集．